Categoria: Tutorials
3. Competenze per programmare: la rappresentazione digitale dei numeri interi e decimali
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 24/03/2024 21:11:45 | in Tutorials
Skill Factory - 24/03/2024 21:11:45 | in Tutorials
I numeri che usiamo si chiamano "Numeri reali", in base alle loro caratteristiche li possiamo organizzare nei seguenti insiemi:

I numeri, sia interi (relativi), sia decimali (razionali), servono per esprimere rispettivamente quantità intere o frazionarie.
Sono irrazionali i numeri che non si possono indicare attraverso il rapporto tra numeri interi, come ad esempio il pi greco, che indica il rapporto tra la misura della circonferenza di un cerchio e il suo diametro oppure il numero di Nepero (e).
In programmazione per indicare la parte decimale di un numero si usa il punto "." al posto della virgola ",", quindi negli esempi userò questa convenzione.
Esempio 1
Per indicare la quantità di auto nell'immagine seguente, basta usare il numero intero 9:

mentre per indicare la quantità di auto nell'immagine seguente, bisogna usare il numero decimale 8.5, perché l'ultima auto è divisa a metà:

Esempio 2
Il risultato dell'espressione 10/2 è 5 che è un numero intero, perché il numero 10 può essere diviso esattamente in due parti intere, ciascuna composta da 5 unità.
Il risultato dell'espressione 10/3 è 3.33333 che è un numero decimale, perché il numero 10 può essere diviso in 3 parti intere, ciascuna composta da 3 unità, ma ne resta una che deve essere frazionata in 3 parti decimali da 0.33333.
Attenti, quando la quantità di cifre decimali di un numero è indefinita, ovvero quando l'unità non è divisibile in parti esattamente uguali, come nel caso del riusultato della divisione 10/3 = 3.33333..., il numero può essere scritto nel modo seguente:
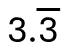
e si legge 3.3 periodico, perché il numero di 3 della parte decimale potrebbe essere infinito.
In programmazione, quando il numero di decimali è periodico, bisogna indicare la precisione del numero ovvero il numero di cifre da indicare dopo la virgola, per questo motivo nei linguaggi di programmazione si fa la distinzione tra numeri decimali a singola precisione (float) e doppia precisione (double). Di solito i numeri a doppia precisione si usano in ambiti scientifici, quelli a singola precisione per tutti gli altri ambiti.
Esempio 3
I numeri si possono anche rappresentare sugli assi cartesiani, come mostra l'immagine seguente:
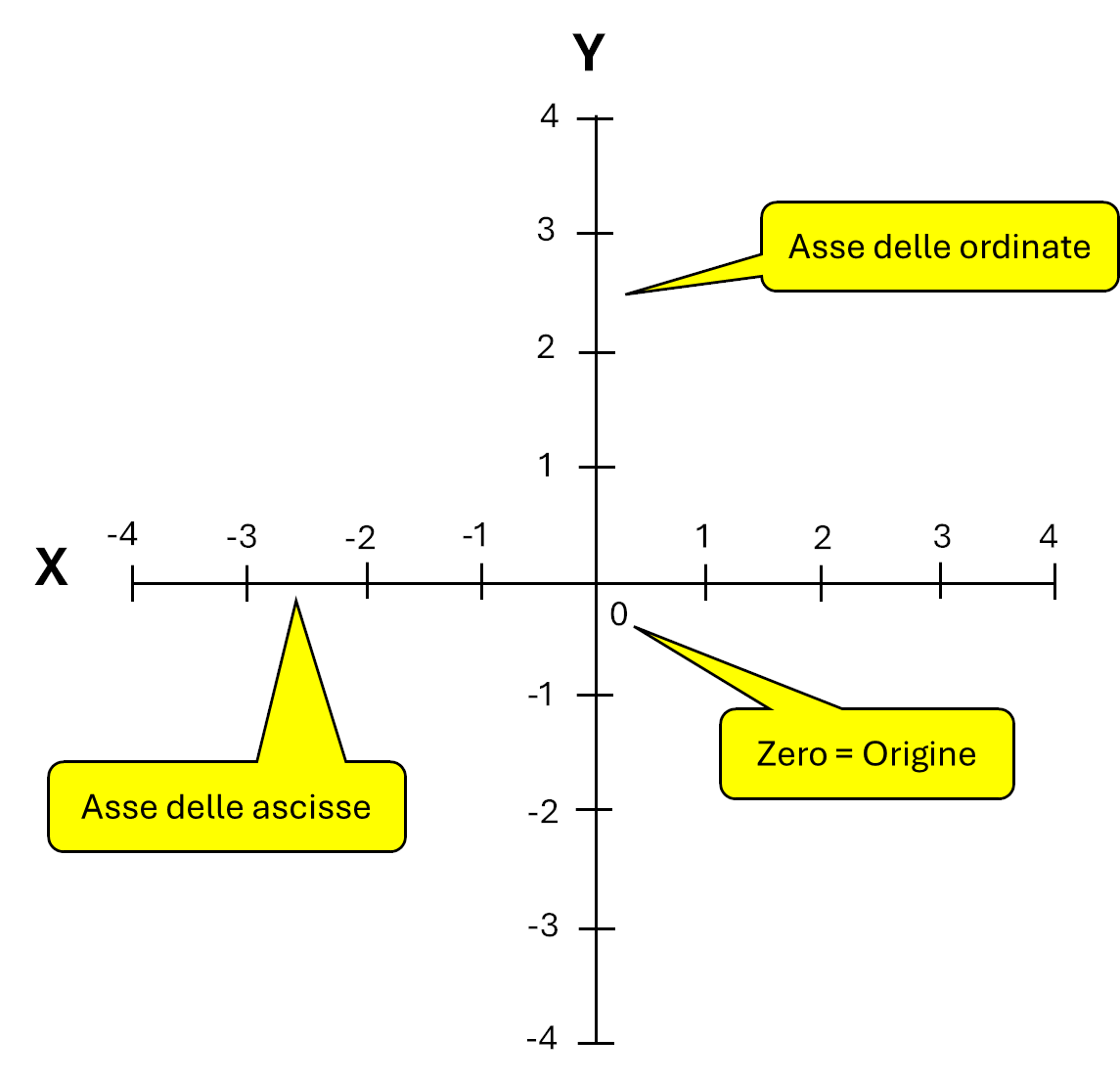
Se l'asse cartesiano è orizzontale si chiama asse delle ascisse e si indica con la lettera X, mentre se è verticale si chiama asse delle ordinate e si indica con la lettera Y.
Un piano su cui si disegna sia l'asse delle "Ascisse", sia l'asse delle "Ordinate" viene detto "Piano Cartesiano".
Il numero 0, si trova nel punto in cui gli assi X e Y s'incontrano e viene chiamato origine. Lo zero divide i numeri positivi (segno +) da quelli negativi (segno -) di entrambi gli assi; sia i numeri positivi, sia i numeri negativi sono infiniti.
Attenti, quando scrivete un numero positivo, non siete obbligati ad indicare il segno +, mentre quando scrivete un numero negativo il segno - è obbligatorio.
Sugli assi cartesiani, la parte decimale di un numero è sempre compresa nel segmento che unisce due numeri interi consecutivi.
L'immagine seguente mostra la posizione del numero 2.5 sull'asse X:
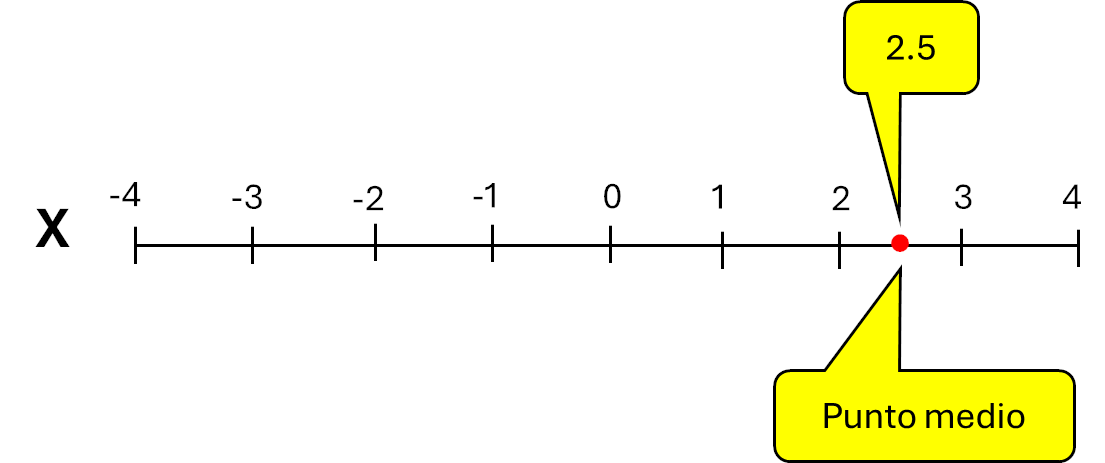
Ricordate che il punto centrale di un segmento che lo divide in due parti uguali è detto punto medio.
L'immagine seguente mostra la posizione del il numero -3.2 sull'asse X:
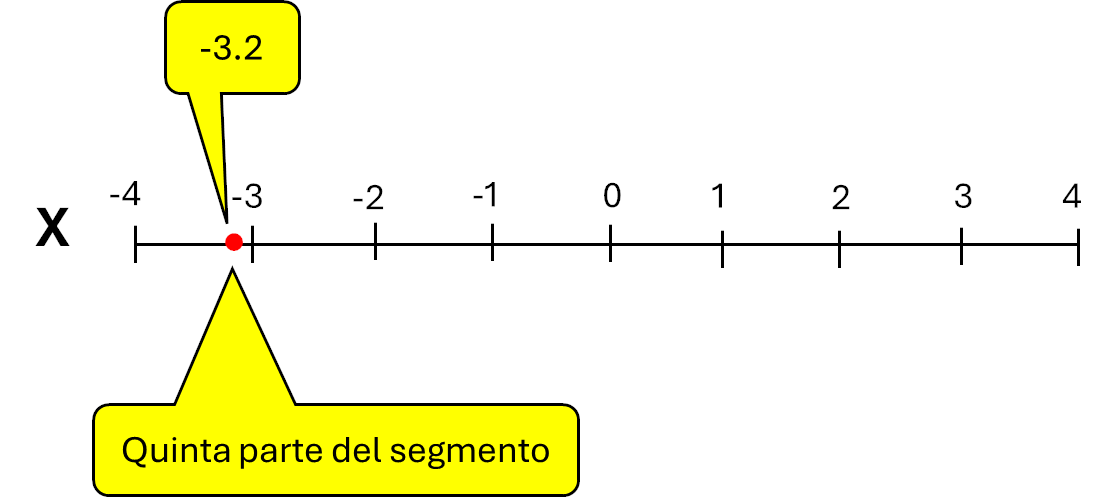
Per indicare la parte decimale 0.2 dovete posizionarvi esattamente nel punto che corrisponde alla quinta parte del segmento, perché 1/5=0.2, come mostra l'immagine.
Come ci ha insegnato il filosofo greco Democrito, un segmento può essere diviso infinite volte, per questo motivo la quantità di cifre decimali di un numero può anche essere molto grande; maggiore è il numero di decimali, tanto maggiore è il numero di volte che vengono divise le parti del segmento. La precisione, ovvero la quantità di cifre decimali di un numero, serve per capire fino a quando dobbiamo continuare dividere le parti del segmento, per evitare di continuare all'infinito.
In che modo i computer memorizzano i numeri interi?
I computer sono macchine elettroniche di tipo digitale, a differenza degli uomini, per scrivere i numeri possono usare solo due cifre: 0 e 1 chiamate bit (binary digit), per questo motivo usano il sistema di numerazione binario.
I computer memorizzano i numeri nella RAM (Random Access Memory); la memoria ad accesso casuale composta da tanti interruttori, chiamati flip-flop, che permettono di scrivere i numeri in forma binaria - se l'interruttore spento (-) la cifra è zero, se è acceso (+) la cifra è uno.

Clicca qui per conoscere la differenza tra mondo reale e mondo digitale.
Nei linguaggi di programmazione le variabili oppure gli oggetti che possono contenere tipi interi si dichiarano con: int oppure Integer, ad esempio:
int x=10;
Integer y=20;
In SQL le colonne di una tabella che possono contenere numeri interi di dichiarano con la parola chiave numeric, ad esempio:
create table magazzino(id numeric(7), quantita numeric(7),...);
Quando un computer memorizza nella RAM un numero intero, usa il primo bit a sinistra (quello più significativo) per indicare il segno; se il primo bit più significativo è 0 il numero intero è positivo, altrimenti è negativo. Gli altri bit servono per indicare il modulo del numero intero.
Per i numeri positivi, il modulo è rappresentato semplicemente dal valore binario del numero da memorizzare.
Per i numeri negativi, il modulo è rappresentato in complemento a 2.
2.147.483.647 = [0](segno)[1111111 11111111 11111111 11111111](modulo = valore binario del numero 2147483647)
–2.147.483.648 = [1](segno)[00000000 00000000 00000000 00000000](modulo = complemento a 2 del numero 2147483648)
Complemento a 2
Per calcolare il complemento a 2 di un numero binario è semplice, basta invertire i valori dei bit, gli zeri diventano uno e gli uno diventano zero e aggiungere 1 al numero che si ottiene.
Ad esempio, il complemento a 2 binario del numero 10 (decimale) si calcola nel modo seguente:
1) converto il numero 10 decimale in binario:
10 (decimale) = 1010 (binario)
2) Calcolo il complemento a 1 del numero 1010 invertendo gli zeri con uno e gli uno con zero:
1010 (binario) = 0101 (complemento a 1)
3) aggiungo 1 al numero 0101:
0101+
0001=
---------
0110 (Complemento a 2 del numero binario 1010)
Allo stesso modo possiamo calcolare il complemento a 2 del numero decimale 2.147.483.648:
1) converto il numero 2.147.483.648 decimale in binario:
2.147.483.648 (decimale) = 10000000 00000000 00000000 00000000 (binario)
2) Calcolo il complemento a 1 del numero 10000000 00000000 00000000 00000000 invertendo gli zeri con uno e gli uno con zero:
10000000 00000000 00000000 00000000 (binario) = 01111111 11111111 11111111 11111111 (complemento a 1)
3) aggiungo 1 al numero 01111111 11111111 11111111 11111111:
01111111111111111111111111111111+
00000000000000000000000000000001=
-----------------------------------------------------------
10000000000000000000000000000000 (Complemento a 2 del numero binario 01111111111111111111111111111111)
...
stipendio decimal(9,2),
...)
La rappresentazione nei computer a virgola fissa è molto semplice: il byte più significativo rappresenta il segno, un certo numero di byte viene utilizzato per rappresentare la parte intera, segue quindi un altro numero di byte per rappresentare la parte decimale, come mostra l'immagine seguente:

Ad esempio, convertiamo in binario il numero decimale 17,55, immaginando di avere 16 bit a disposizione:
1) Il bit più significativo è uguale a 0, perché il numero è positivo.
2) La parte intera, immaginiamola di 7 bit, è uguale a:
2^6=64 -> 0
2^5=32 -> 0
2^4=16 -> 1
2^3=8 -> 0
2^2=4 -> 0
2^1=2 -> 0
2^0=1 -> 1
17 (decimale) = 0010001 (binario)
Se la parte intera fosse stata negativa avremmo dovuto calcolare il complemento a 2.
3) La parte decimale, immaginandola di 8 bit, è uguale a:
2^-1=0.5 -> 1
2^-2=0.25 -> 0
2^-3=0.125 -> 0
2^-4=0.0625 -> 0
2^-5=0.03125 -> 1
2^-6=0,015625 -> 1
2^-7=0,0078125 -> 0
2^-8=0,00390625 -> 0
0.55 (decimale) = 10001100 (binario)
Quindi
17.55 (decimale) =0(segno) 0010001.10001100

bit 31 (1) segno
bit 23-30 (8) esponente
bit 0-22 (23) mantissa
mentre per la precisione doppia l'organizzazione è la seguente:
bit 63 (1) segno
bit 52-62 (11) esponente
bit 0-51 (52) mantissa

INFORMATICA APPLICATA
Laboratorio
Creare un programma che trasforma i numeri interi nella rappresentazione binaria a 32 bit usata dai computer per memorizzare le informazioni numeriche.
Soluzione JavaScript
// Funzioni
function convertiBinario(numeroIntero){
let numeroBinario=[]
let resto
while (numeroIntero>1){
resto=numeroIntero%2
numeroBinario.push(resto)
numeroIntero=Math.floor(numeroIntero/2)
}
numeroBinario.push(numeroIntero)
for(let i=31-numeroBinario.length;i>0;i--){
numeroBinario.push(0)
}
numeroBinario.reverse()
return numeroBinario
}
function complemento2(numeroBinario){
let inverti=[1,0]
riporto=1
for (let i=0;i<numeroBinario.length;i++){
numeroBinario[i]=inverti[numeroBinario[i]]
}
for(let i=numeroBinario.length-1;i>0;i--){
if (numeroBinario[i]==1 && riporto==1){
numeroBinario[i]=0
riporto=1
}else if (numeroBinario[i]==1 && riporto==0){
numeroBinario[i]=1
riporto=0
}else if (numeroBinario[i]==0 && riporto==1){
numeroBinario[i]=1
riporto=0
}else{
numeroBinario[i]=0
riporto=0
}
}
}
// Programma
let input=require("readline-sync");
let numeroIntero=0
let numeroBinario=[]
let numeroBinarioStr=""
let segno=0
numeroIntero=parseInt(input.question("Numero intero: "))
while (numeroIntero<-2147483648 || numeroIntero> 2147483647){
print("Errore: inserire un numero compreso tra -2147483648 e 2147483647")
numeroIntero=parseInt(input.question("Numero intero: "))
}
if (numeroIntero<0){
segno=1
numeroBinario=convertiBinario(-(numeroIntero))
complemento2(numeroBinario)
}
else if (numeroIntero>0){
segno=0
numeroBinario=convertiBinario(numeroIntero)
}
numeroBinarioStr="["+segno+"]["
for (let i=0;i<numeroBinario.length;i++){
if (i<31){
numeroBinarioStr+=numeroBinario[i]
}
}
numeroBinarioStr+="]"
console.log(numeroBinarioStr)
Soluzione Python
# Funzioni
# Converte numero intero in binario
def convertiBinario(numeroIntero):
numeroBinario=[]
while numeroIntero>1:
resto=numeroIntero%2
numeroBinario.append(resto)
numeroIntero=int(numeroIntero/2)
numeroBinario.append(numeroIntero)
for i in range(31-len(numeroBinario)):
numeroBinario.append(0)
numeroBinario.reverse()
return numeroBinario
# Calcola il complemento a due di un numero binario
def complemento2(numeroBinario):
inverti=[1,0]
riporto=1
for i in range(len(numeroBinario)):
numeroBinario[i]=inverti[numeroBinario[i]]
for i in range(len(numeroBinario)-1,0,-1):
if numeroBinario[i]==1 and riporto==1:
numeroBinario[i]=0
riporto=1
elif numeroBinario[i]==1 and riporto==0:
numeroBinario[i]=1
riporto=0
elif numeroBinario[i]==0 and riporto==1:
numeroBinario[i]=1
riporto=0
else:
numeroBinario[i]=0
riporto=0
# Programma
numeroIntero=0
numeroBinario=[]
segno=0
numeroIntero=int(input("Numero intero: "))
while numeroIntero<-2147483648 or numeroIntero> 2147483647:
print("Errore: inserire un numero compreso tra -2147483648 e 2147483647")
numeroIntero=int(input("Numero intero: "))
if numeroIntero<0:
segno=1
numeroBinario=convertiBinario(-(numeroIntero))
complemento2(numeroBinario)
elif numeroIntero>0:
segno=0
numeroBinario=convertiBinario(numeroIntero)
print("["+str(segno)+"][",end="")
for i,x in enumerate(numeroBinario):
if i<31: print(x,end="")
print("]")
Leggi anche le altre lezioni ...
COMPETENZE PER PROGRAMMARE:
1-I sistemi di numerazione
2-Mondo reale e Mondo Digitale
4-Le stringhe
5-Le espressioni regolari (REGEXP)
6-Date, ore e fusi orari
Segui sul canale YouTube "Skill Factory Channel" la Playlist: COMPETENZE PER PROGRAMMARE
TUTORIALS
1-Laboratori di logica di programmazione in C
2-Impariamo a programmare con JavaScript
3-Ricominciamo dal linguaggio SQL
4-Introduzione alla logica degli oggetti
5-TypeScript
6-Impariamo a programmare in Python
7-Come sviluppare un sito in WordPress
PAR GOL (Garanzia di Occupabilità dei Lavoratori)

Se sei residente in Campania e cerchi lavoro, sai che puoi partecipare gratuitamente ad un corso di formazione professionale PAR GOL?
I corsi di formazione professionale PAR GOL sono finanziati dalla Regione Campania e ti permettono di acquisire una Qualifica Professionale Europea (EQF) e di partecipare ad un tirocinio formativo aziendale.
Invia il tuo CV o una manifestazione d'interesse a: recruiting@skillfactory.it
oppure
chiama ai seguenti numeri di telefono:
Tel.: 081/18181361
Cell.: 327 0870141
oppure
Contattaci attraverso il nostro sito: www.skillfactory.it
Per maggiori informazioni sul progetto PAR GOL, clicca qui.
Per maggiori informazioni sulle Qualifiche Professionali Europee (EQF), clicca qui.
Academy delle professioni digitali
Per consultare il catalogo dei corsi online della nostra Academy ...

... collegati al nostro sito: www.skillfactory.it
2. Competenze per programmare: Mondo Reale e Mondo Digitale
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 25/02/2023 10:16:25 | in Tutorials
Skill Factory - 25/02/2023 10:16:25 | in Tutorials

Nell'era della trasformazione digitale è importante capire la differenza tra "Mondo reale" e "Mondo digitale".
Oggi, mondo reale e mondo digitale, coesistono, ampliando lo spazio fisico in cui viviamo con quello cibernetico, che può essere considerato come un Universo parallelo, alternativo a quello fisico.
Il mondo reale è quello in cui viviamo, composto dalle cose che osserviamo e tocchiamo, quello digitale è il mondo delle cose che assumono la forma di numeri binari.
Il mondo digitale esiste grazie al Ciberspazio (Cyberspace), la rete delle reti, chiamta Internet, che interconnette tutti i sistemi informatici ed elettronici del mondo, su cui girano i software e le applicazioni che permettono il funzionamento di Internet e del mondo cibernetico.

Il termine è stato utilizzato la prima volta nel 1982, nella forma inglese cyberspace, in un racconto di fantascienza dal titolo "Burning Chrome".
I tipi di applicazioni più conosciuti del cyberspace sono i seguenti:
- Social media;
- Social network;
- Motori di ricerca;
- Portali;
- Siti Web;
- Blog;
- E-Commerce;
- E-Learning
- Community;
- Suite applicative;
- Etc..
Qual è la diiferenza tra mondo reale e mondo digitale?
La risposta è semplice, il mondo reale è fatto di informazioni analogiche, quello digitale è fatto di cifre binarie, perché gli apparecchi elettronici possono gestire solo due stati fisici (flip-flop), che noi identifichiamo con le cifre 0 e 1, chiamate bit (Binary Digit).

Come sono fatte le informazioni analogiche?
Tutto cio che percepiamo nel mondo reale ha una forma analogica. Senza scendere in tenicismi complessi, possiamo dire che tutto quello che vedete o ascoltate, sotto forma di immagini o suoni, fatto di punti, linee oppure onde, è analogico.
Gli apparecchi elettronici, a differenza degli uomini, non possono memorizzare le immagini e i suoni in forma analogica, ma lo possono fare in forma digitale; sequenze di cifre binarie chiamate bit.
Fisicamente i bit negli apparecchi elettronici corrispondono a sequenze di interruttori (Flip-Flop) che possono assumere lo stato 0 oppure 1.
La cosa importante è che qualunque informazione analogica può essere trasformata in digitale e viceversa.
E' vero che le informazioni digitali sono più precise di quelle analogiche?
Si, è vero. I numeri sono grandezze precise, le immagini e i suoni possono anche essere interpretati male; questo è evidente con gli orologi.
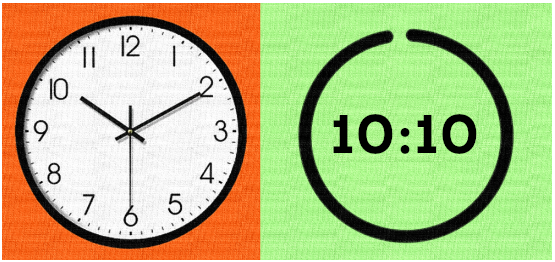
Un orologio anlagico indica le ore, i minuti e i secondi attraverso tre lancette diverse, la posizione delle lancette, quando viene letta l'ora, può essere interpretata male e la persona potrebbe leggere un informazione non esatta.
Un orologio digitale indica le ore, i minuti e i secondi attraverso cifre, in questo caso l'ora letta è sempre esatta.
In che modo le informazioni analogiche possono essere trasformate in digitali?
La risposta a questa domanda complessa, può diventare semplice se facciamo riferimento all'informatica.
Quando scrivete qualcosa con un dispositivo elettronico, utilizzate la tastiera:

Tutti i caratteri della tastiera, noi li percepiamo come informazioni analogiche, perchè sono composti da punti e linee, quindi il testo che scriviamo noi lo possiamo ricordare, il dispositivo che stiamo usando no.
Per permettere al dispositivo elettronico di memorizzare i caratteri usati per scrivre un testo, devono essere convertiti in numeri; per questo motivo è nata la tabella dei codici ASCII (pronuncia ASKII) che associa a 256 caratteri diversi, un numero da 0 a 255:
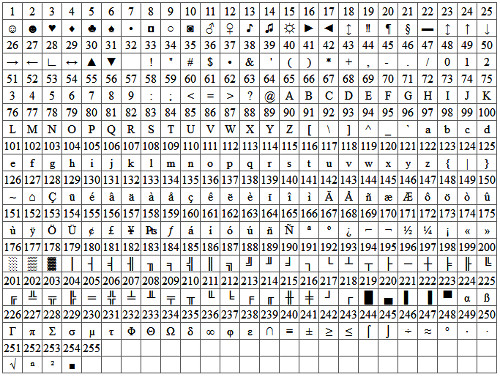
Per approfondire la conoscenza del codice ASCII clicca qui.
Ad esempio, se digitate un carattere "A" oppure un carattere "1", entrabi vengono prima convertiti nei rispettivi codici ASCII 65 e 49, successivamente i numeri decimali vengono convertiti in banario, per permettere al dispositivo elettronico di memorizzarli attraverso sequenze di 8 flip-flop (interruttori elettrici), capaci di rappresentare i bit 0 oppure 1:
A=6510=010000012
1=4910=001100012
L'immagine seguente mostra le fasi di conversione di un messaggio ti tipo testo in binario:
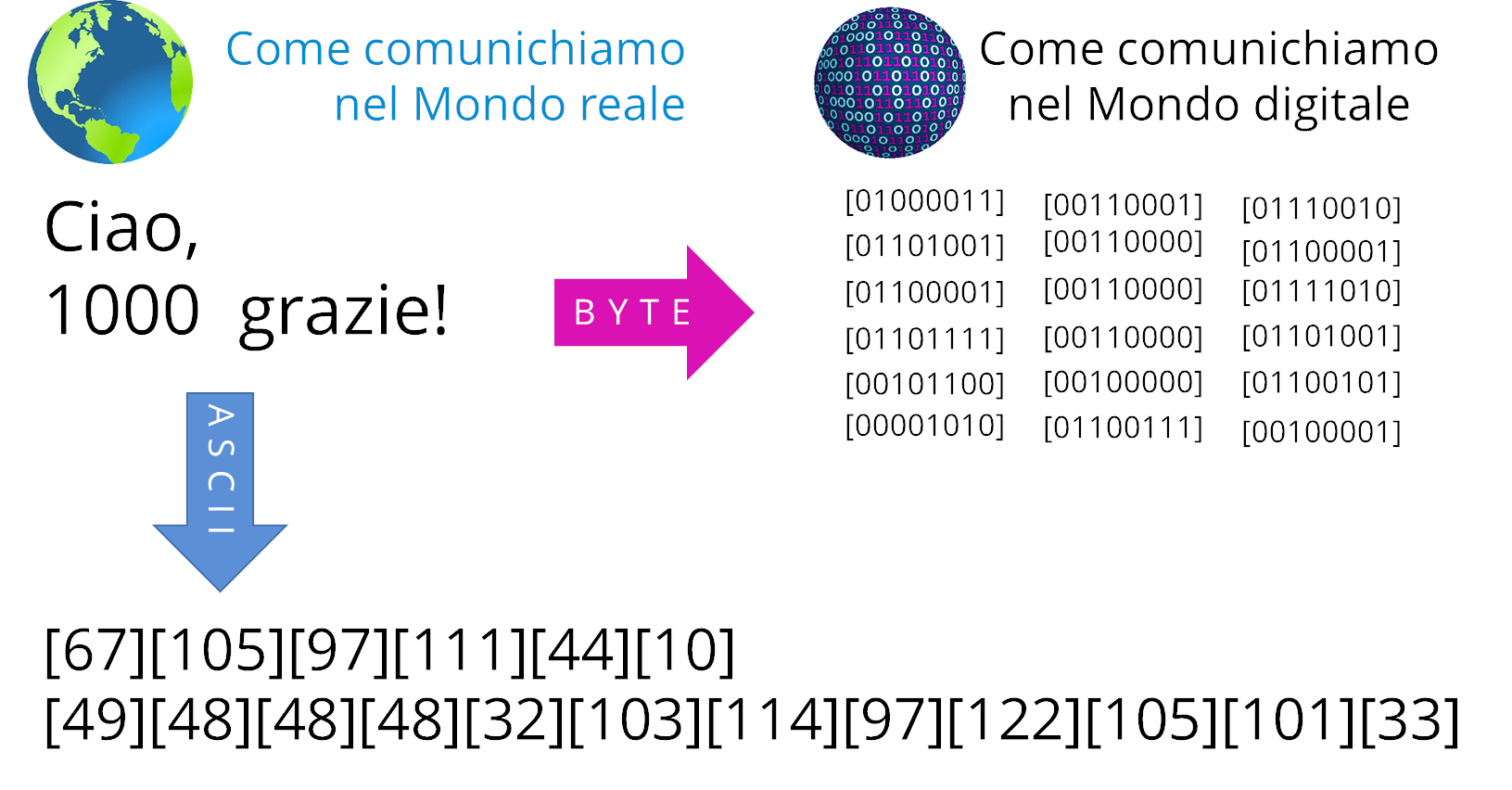
Ricordate che per indicare in binario il numero 255, che corrisponde all'ultimo carattere del codice ASCII, servono otto cifre (bit); per questo motivo l'unità di misura minima dell'informatica è il byte (8 bit).
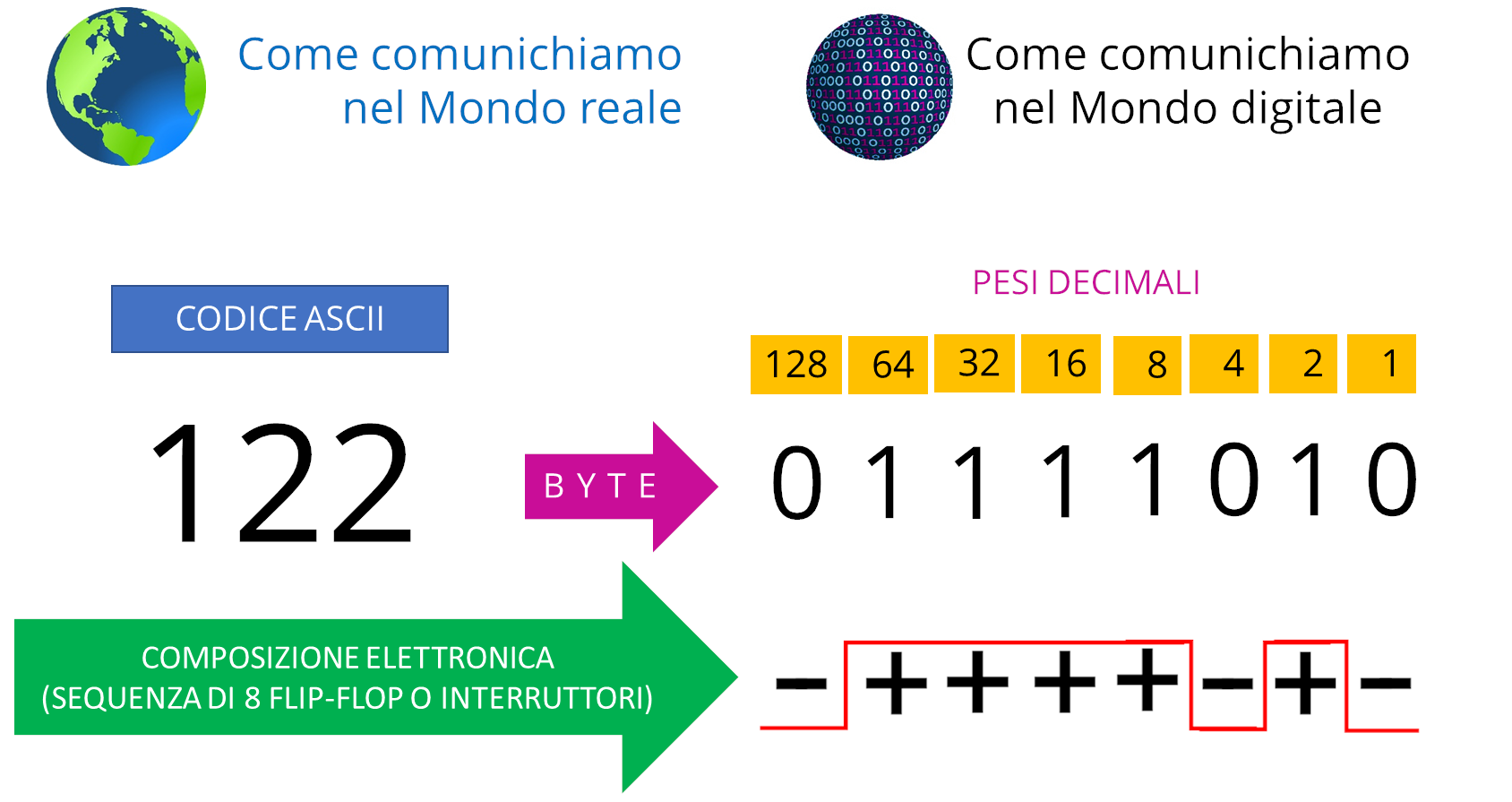
Anche le immagini composte da punti o linee e i suoni formati da onde sinusoidali, possono essere convertiti in sequenze di byte, in questo modo possono essere memorizzati dai dispositivi elettronici.
L'immagine seguente mostra forme diverse di onde sonore in forma analogica:

PRINCIPALI STRUMENTI DEL MONDO REALE E DEL MONDO DIGITALE
- COLORI

- IMMAGINI

- SUONI

- POSTA

- LIBRI

- CHIAVI

- FIRME

- SOLDI

- MAGAZZINO

IDENTITA' DIGITALE
- INTELLIGENZA ARTIFICIALE

- REALTA AUMENTATA O METAVERSO

Quali rischi corriamo quando siamo connessi al mondo digitale?
Come per il modo reale, anche in quello digitale si corrono dei rischi, quindi bisogna stare molto attenti a non assumere comportamenti sbagliati.
Quando siete connessi ad Internet con la vostra identità digitale e comunicate con qualcuno, state attenti, perché non sempre chi sta dall'altra parte è realmente chi dice di essere!!!
Non fidatevi di chi vi propone cose strane, ma soprattutto prima di fare qualunque cosa che vi viene richiesta, confidatevi con qualcuno molto vicino a voi.
Un altro rischio molto diffuso quando siete interconnessi ad Internet, è quello del furto d'informazioni riservate come ad esempio:
- Carta d'identità;
- Informazioni di genere, politiche, religiose;
- Password di carte di credito, bmt, conti correnti, etc..
Questa attività, chiamata "Phishing", spesso avviene attraverso l'installazione sul proprio computer di software malevoli, chiamati malware.
Per evitare questo tipo di attacchi, bisogna installare sul proprio computer un buon antivirus, non aprire allegati di mail sospette e non navigare su siti non conosciuti.

Infine attenti ai bulli, perché potreste trovarli anche nel mondo digitale.
Purtroppo in Internet, il fenomeno del cyberbullismo è molto comune; sia nella vita reale, sia in quella digitale. Anche se avete paura non dovete mai subire minacce da parte di altre persone, le conseguenze potrebbero essere molto gravi.
Se siete vitteme o conoscete qualcuno che è vittima di bullismo o cyberbullismo, è sempre meglio denunciare subito l'accaduto a qualcuno molto vicino a voi o alla polizia!!!

INFORMATICA APPLICATA
Laboratorio
Creare un programma che trasforma un messaggio di tipo testo in ASCII e in binario (Byte).
Soluzione JavaScript
// Funzioni
function decimaleBinario(decimale) {
var binario = [];
var numero = 0;
var posizione = 7;
for (var x = 0; x < 8; x++) {
binario.push(0);
}
numero = decimale;
while (numero >= 2) {
risultato = Math.floor(numero / 2);
resto = numero % 2;
binario[posizione] = resto;
posizione--;
numero = risultato;
}
binario[posizione] = numero;
return binario.join('');
}
// Programma
var input = require("readline-sync");
var messaggio = "";
var risposta = "";
var riga = "";
var ascii = [];
var binario = [];
var x = 0;
do {
ascii = [];
binario = [];
messaggio = input.question("Messaggio da convertire: ");
for (var x = 0; x < messaggio.length; x++) {
ascii.push(messaggio.charCodeAt(x));
binario.push(decimaleBinario(messaggio.charCodeAt(x)));
}
console.log("Conversione del messaggio in ASCII:");
riga = "";
for (x = 0; x < ascii.length - 1; x++) {
riga = riga + ascii[x] + ","
}
riga = riga + ascii[x] + "."
console.log(riga);
console.log("Conversione del messaggio in binario (Byte):");
riga = "";
for (x = 0; x < binario.length - 1; x++) {
riga = riga + binario[x] + ","
}
riga = riga + binario[x] + "."
console.log(riga);
risposta = input.question("Vuoi inserire un altro messaggio (s/n)? ")
while (risposta.toLowerCase() != 's' && risposta.toLowerCase() != 'n') {
console.log("Errore: inserire s oppure n.");
risposta = input.question("Vuoi inserire un altro messaggio (s/n)? ")
}
} while (risposta.toLowerCase() == 's');
Soluzione Python
import math
# Funzioni
def decimaleBinario(decimale):
binario = []
numero = 0
posizione = 7
for x in range(8):
binario.append('0')
numero = decimale
while numero >= 2:
risultato = math.floor(numero / 2)
resto = numero % 2
binario[posizione] = str(resto)
posizione = posizione-1
numero = risultato
binario[posizione] = str(numero)
return ''.join(binario)
# Programma
messaggio = ''
risposta = 's'
riga = ''
ascii = []
binario = []
x = 0
while risposta == 's':
ascii = []
binario = []
messaggio = input("Messaggio da convertire: ")
for carattere in messaggio:
ascii.append(ord(carattere))
binario.append(decimaleBinario(ord(carattere)))
print("Conversione del messaggio in ASCII:")
riga = ""
for x in range(len(ascii)-1):
riga = riga + str(ascii[x]) + ","
x=x+1
riga = riga + str(ascii[x]) + "."
print(riga)
print("Conversione del messaggio in binario (Byte):")
riga = ""
for x in range(len(binario)-1):
riga = riga + binario[x] + ","
x=x+1
riga = riga + binario[x] + "."
print(riga)
risposta = input("Vuoi inserire un altro messaggio (s/n)? ")
while risposta != 's' and risposta != 'n':
print("Errore: inserire s oppure n.")
risposta = input("Vuoi inserire un altro messaggio (s/n)? ")
Come eseguire il programma JavaScript
Per eseguire il programma JavaScript, bisogna installare il framework node.js sul proprio computer.
Il download del file d'installazione può essere fatto collegandosi al link: https://nodejs.org/it/download/.
Il file di download deve corrispondere al sistema operativo installato sul proprio computer.
Dopo il download eseguire il file per installare node.js.
Per verificare se il framework node.js è stato installato correttamente, dal prompt dei comandi del sistema operativo usato, eseguire il comando:
node --version
dovrebbe essere visualizzata la versione di node.js installata, come mostra l'immagine seguente:
Successivamente bisogna creare una cartella "laboratori" dove salvare il programma JavaScript da eseguire.
Per salvare il programma nella cartella "laboratori", basta copiarlo nel blocco note o in qualunque editor di testo e salvarlo con il nome:
analogico_digitale.js
Infine, da prompt dei comandi, entrare nella cartella laboratori ed eseguire il comando:
npm install readline-sync
Questa libreria serve per permettere l'inserimento di dati da tastiera, quando viene eseguito il programma.
A queso punto si può eseguire il programma con il comando node, che è l'interprete JavaScript di node.js, come mostra l'esempo seguente:
node analogico_digitale
Come eseguire il programma Python
Per eseguire il programma Python, bisogna installare il framework python sul proprio computer.
Il download del file d'installazione può essere fatto collegandosi al link: https://www.python.org/downloads/.
Il file di download deve corrispondere al sistema operativo installato sul proprio computer.
Dopo il download eseguire il file per installare python.
Attenzione, durante l'installazione è importante spuntare l'opzione "Add Python 3.X to PATH:
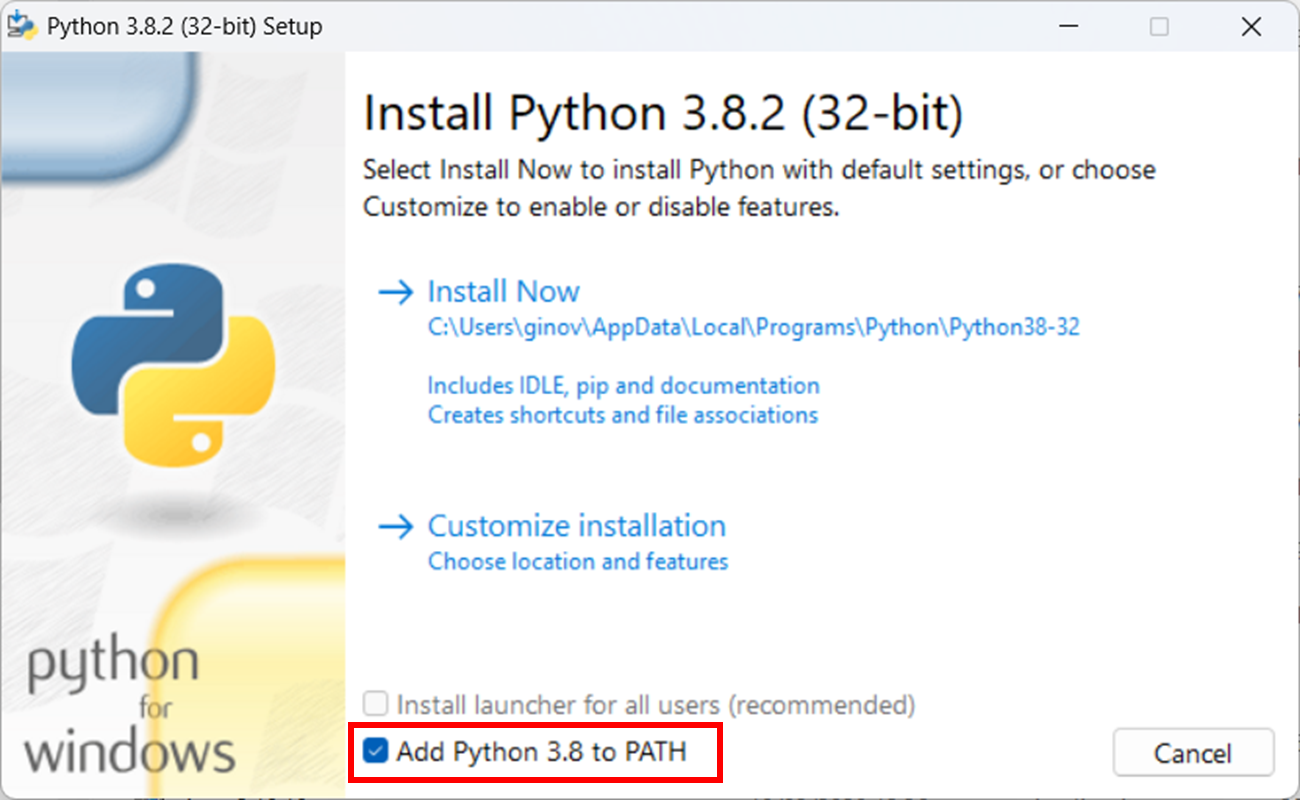
Per verificare se il framework python è stato installato correttamente, dal prompt dei comandi del sistema operativo usato, eseguire il comando:
python --version
dovrebbe essere visualizzata la versione di python installata, come mostra l'immagine seguente:
Successivamente bisogna creare una cartella "laboratori" dove salvare il programma python da eseguire.
Per salvare il programma nella cartella "laboratori", basta copiarlo nel blocco note o in qualunque editor di testo e salvarlo con il nome:
analogico_digitale.py
Infine, da prompt dei comandi, entrare nella cartella laboratori ed eseguire il comando:
python analogico_digitale.py
Leggi anche le altre lezioni ...
COMPETENZE PER PROGRAMMARE:
1-I sistemi di numerazione
3-La reppresentazione digitale dei numeri interi e decimali
4-Le stringhe
5-Le espressioni regolari (REGEXP)
6-Date, ore e fusi orari
Segui sul canale YouTube "Skill Factory Channel" la Playlist: COMPETENZE PER PROGRAMMARE
TUTORIALS
1-Laboratori di logica di programmazione in C
2-Impariamo a programmare con JavaScript
3-Ricominciamo dal linguaggio SQL
4-Introduzione alla logica degli oggetti
5-TypeScript
6-Impariamo a programmare in Python
7-Come sviluppare un sito in WordPress
PAR GOL (Garanzia di Occupabilità dei Lavoratori)

Se sei residente in Campania e cerchi lavoro, sai che puoi partecipare gratuitamente ad un corso di formazione professionale PAR GOL?
I corsi di formazione professionale PAR GOL sono finanziati dalla Regione Campania e ti permettono di acquisire una Qualifica Professionale Europea (EQF) e di partecipare ad un tirocinio formativo aziendale.
Invia il tuo CV o una manifestazione d'interesse a: recruiting@skillfactory.it
oppure
chiama ai seguenti numeri di telefono:
Tel.: 081/18181361
Cell.: 327 0870141
oppure
Contattaci attraverso il nostro sito: www.skillfactory.it
Per maggiori informazioni sul progetto PAR GOL, clicca qui.
Per maggiori informazioni sulle Qualifiche Professionali Europee (EQF), clicca qui.
Academy delle professioni digitali
Per consultare il catalogo dei corsi online della nostra Academy ...

... collegati al nostro sito: www.skillfactory.it
1. Competenze per programmare: i sistemi di numerazione
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 19/02/2023 17:01:17 | in Tutorials
Skill Factory - 19/02/2023 17:01:17 | in Tutorials

Introduzione ai sistemi di numerazione
I sistemi di numerazione più usati nell'ambito informatico sono:
1) il sistema decimale a base 10 perché per comporre i numeri utilizza le cifre (0,1,2,3,4,5,6,7,8,9)
2) il sistema binario a base 2 perché per comporre i numeri utilizza le cifre (0,1) chiamate bit (binary digit)
3) il sistema ottale a base 8 perché per comporre i numeri utilizza le cifre (0,1,2,3,4,5,6,7)
4) il sistema esadecimale a base 16 perché per comporre i numeri utilizza le cifre (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F)
Il sistema decimale (dec) è quello usato dagli uomini, che contando con le dieci dita delle mani trovano più conveniente usare dieci cifre.

Il sistema binario (bin) è quello usato dai computer, che per contare hanno solo due stati, acceso=1 o spento=0, che corrispondono a interruttori elettronici chiamati flip-flop.

Sequenze di flip-flop (interruttori elettronici a due stati spento=0 e acceso=1) permettono di scrivere i numeri in forma binaria, ovvero come sequenze di bit (0/1).
I numeri binari sono difficili da ricordare perché sono composti da troppe cifre, per questo motivo spesso vengono convertiti in ottale (ott o oct) oppure in esadecimale (esa o hex).
Ad esempio, numeri binari composti da tre bit possono essere rappresentati con una sola cifra ottale:
[Bin] [Ott]
000 = 0
001 = 1
010 = 2
011 = 3
100 = 4
101 = 5
110 = 6
111 = 7
Se i numeri binari sono composti da quattro bit, allora conviene rappresentarli con una cifra esadecimale, come mostra l'esempio seguente:
[Bin] [Esa]
0000 = 0
0001 = 1
0010 = 2
0011 = 3
0100 = 4
0101 = 5
0110 = 6
0111 = 7
1000 = 8
1001 = 9
1010 = A
1011 = B
1100 = C
1101 = D
1110 = E
1111 = F
In informatica l'unità minima di misura è il byte che corrisponde ad otto bit. Questo significa che qualunque apparecchio elettronico quando legge o scrive i numeri binari lo fa con otto bit contemporaneamente.
Per rappresentare il valore di un byte composto da otto cifre binarie (bit), bastano semplicemente due cifre esadecimali.
Ad esempio:
[Byte] [Esa]
00000000 = 00
00000001 = 01
00001111 = 0F
00010000 = 10
11111111 = FF
Che cosa sono i numeri
Nell'ambito informatico capire che cosa sono i numeri è fondamentale per comprendere i sistemi di numerazione.
Tutti i numeri indipendentemente dal sistema di numerazione scelto indicano quantità di unità oppure di cose.
Ad esempio, il numero 9 decimale potrebbe indicare un insieme di nove auto:

Per indicare un insieme di nove auto in ottale il numero sarebbe 11, mentre in binario sarebbe 1001.
Come mai numeri diversi indicano la stessa quantità di cose?
Per rispondere a questa domanda dobbiamo capire che cos'è il sistema posizionale.
Il sistema posizionale
Il sistema posizionale definisce le regole da applicare per capire la quantità di unità oppure cose indicata da un numero.
Prima di tutto è importante definire il sistema di numerazione usato per scrivere i numeri, perché in questo modo possiamo conoscere il numero di cifre disponibili.
Il numero di cifre usate da un sistema di numerazione si chiama base, ad esempio la base del sistema decimae è uguale a 10 perché usa dieci cifre: 0,1,2,3,4,5,6,7,8,9.
La base del sistema esadecimale è uguale a 16 perché questo sistema usa sedici cifre: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E;F.
Attenzione le cifre A,B,C,D,E,F se le trovate in un calcolo valogno rispettivamente: 10,11,12,13,14,15.
Per capire a quale sistema di numerazione appartiene un numero, basta indicare la base come pedice, come mostra l'esempio seguente:
910
118
10012
Tutti e tre i numeri indicano 9 unità.
La prima regola del sistema posizionale ci dice che le cifre di un numero possono indicare quantità di unità diverse in base alla loro posizione nel numero; per questo motivo si parla di sistema posizionale.
Per conoscere la quantità di unità indicata da ogni cifra in un numero, bisogna moltiplicare le cifra per un valore detto peso. I valori dei pesi cambiano in base alla posizione della cifra nel numero e in base al sistema di numerazione usato.
Per ottenere i valori dei pesi corrispondenti alle posizioni delle cifre in un numero, basta calcolare la potenza seguente:
base(posizione-1)
dove base indica il numero di cifre del sistema di numerazione usato e posizione indica dove si trova la cifra nel numero.
Per il sistema decimale, la base è 10, quindi i pesi sono i seguenti:
Posizione Base Esponente Peso
1 10 1-1=0 1
2 10 2-1=1 10
3 10 3-1=2 100
4 10 4-1=3 1000
In realtà i pesi del sistema decimale sono le unità (U), le decine (D), le centinaia (C), le migliaia (M), etc., che impariamo a scuola quando facciamo la scomposizione dei numeri.
Per il sistema binario, la base è 2, quindi i pesi sono i seguenti:
Posizione Base Esponente Peso
1 2 1-1=0 1
2 2 2-1=1 2
3 2 3-1=2 4
4 2 4-1=3 8
5 2 5-1=4 16
6 2 6-1=5 32
7 2 7-1=6 64
8 2 8-1=7 128
Per il sistema ottale, la base è 8, quindi i pesi sono i seguenti:
Posizione Base Esponente Peso
1 8 1-1=0 1
2 8 2-1=1 8
3 8 3-1=2 64
4 8 4-1=3 512
Per il sistema esadecimale, la base è 16, quindi i pesi sono i seguenti:
1 16 1-1=0 1
2 16 2-1=1 16
3 16 3-1=2 256
4 16 4-1=3 4096
Adesso che conosciamo i pesi di tutti i sistemi di numerazione, possiamo fare un esempio.
Il numero decimale 255 indica duecentocinquanta cinque unità o cose, come mostra il calcolo seguente:
5 x 1 = 5
5 x 10 = 50
2 x 100 = 200
--------------------
5+50+200=255 unità
Dimostrare che i numeri 111111112 , 3778 e FF16 , indicano lo stesso numero di unità del numero 25510.
Sistema binario: 11111111
1 x 1 = 1
1 x 2 = 2
1 x 4 = 4
1 x 8 = 8
1 x 16 = 16
1 x 32 = 32
1 x 64 = 64
1 x 128 = 128
------------------------
1+2+4+8+16+32+64+128=255 unità
Sistema ottale: 377
7 x 1 = 7
7 x 8 = 56
3 x 64 = 192
------------------------
7+56+192=255 unità
Sistema esadecimale: FF
In questo caso per fare una verifica dovete ricordare che le cifre esadecimali A, B, C, D, E, F, corrispondono ai numeri seguenti:
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15
Quindi
F x 1 = 15 x 1 = 15
F x 16 = 15 x 16 = 240
------------------------
15+240=255 unità
Come si convertono i numeri decimali in numeri binari, ottali ed esadecimali
Per convertire un numero decimale nel numero corrispondente ad un sistema di numerazione diverso, basta procedere nel modo seguente:
1) Definire la base del sistema di numerazione in cui volete convertire il numero decimale;
2) Dividere il numero decimale per la base del sistema di numerazione scelto fino a quando è possibile;
3) Infine, prendere l'ultimo risultato ottenuto, insieme ai resti di tutte le divisioni fatte e scriverli da sinista verso destra.
Ad esempio, convertiamo il numero decimale 255 in binario, ottale e esadecimale.
1) Sistema binario
base=2, segue:
255/2 = 127 con resto 1
127/2 = 63 con resto 1
63/2 = 31 con resto 1
31/2 = 15 con resto 1
15/2 = 7 con resto 1
7/2 = 3 con resto 1
3/2 = 1 con resto 1
da cui si ottiene che:
25510 = 111111112
2) Sistema ottale
base=8, segue:
255/8 = 31 con resto 7
31/8 = 3 con resto 7
da cui si ottiene che:
25510 = 3778
3) Sistema esadecimale
base=16, segue:
255/16 = 15 con resto 15
da cui si ottiene che:
25510 = 151516 = FF16
Matematica applicata
Laboratorio 1
Creare un programma che calcola i primi otto pesi dei seguenti sistemi di numerazione:
1) Decimale (Dec)
2) Binario (Bin)
3) Ottale (Ott)
4) Esadecimale (Esa)
Soluzione JavaScript
var input = require("readline-sync");
var base = 0;
var nomeSistemaDiNumerazione = "";
var risposta = "";
var scelta = 0;
do {
// Menu per la scelta del sistema di numerazione
console.log("1) Sistema Decimale (Dec)");
console.log("2) Sistema Binario (Bin)");
console.log("3) Sistema Ottale (Ott)");
console.log("4) Sistema Esadecimale (Esa)");
console.log("5) Esci");
scelta = parseInt(input.question("Scegli: "))
// Visualizzo un errore se la scelta non è corretta
while (scelta < 1 || scelta > 5 || isNaN(scelta)) {
console.log("Errore:scegli un numero tra 1 e 5 ...");
scelta = input.question("Scegli: ");
}
// Imposto la base e il nome del sistema di numerazione scelto
if (scelta == 1) {
base = 10;
nomeSistemaDiNumerazione = "Decimale (Dec)";
} else if (scelta == 2) {
base = 2;
nomeSistemaDiNumerazione = "Binario (Bin)";
} else if (scelta == 3) {
base = 8;
nomeSistemaDiNumerazione = "Ottale (Ott)";
} else if (scelta == 4) {
base = 16;
nomeSistemaDiNumerazione = "Esadecimale (Esa)";
}
if (scelta != 5) {
// Calcolo i primi 8 pesi in base al sistema di numerazione scelto
console.log("Pesi delle prime 8 cifre di un numero " + nomeSistemaDiNumerazione);
for (x = 0; x <= 7; x++) {
console.log((x + 1) + ") " + Math.pow(base, x));
}
risposta = input.question("Premi invio per continuare ...");
}
} while (scelta != 5);
console.log("Fine programma");
Soluzione Python
import math
base = 0
nomeSistemaDiNumerazione = ''
risposta = ''
scelta = 0
while scelta != 5:
# Menu per la scelta del sistema di numerazione
print("1) Sistema Decimale (Dec)")
print("2) Sistema Binario (Bin)")
print("3) Sistema Ottale (Ott)")
print("4) Sistema Esadecimale (Esa)")
print("5) Esci")
scelta = int(input("Scegli: "))
# Visualizzo un errore se la scelta non è corretta
while scelta < 1 or scelta > 5:
print("Errore:scegli un numero tra 1 e 5 ...")
scelta = int(input("Scegli: "))
# Imposto la base e il nome del sistema di numerazione scelto
if scelta == 1:
base = 10
nomeSistemaDiNumerazione = 'Decimale (Dec)'
elif scelta == 2:
base = 2
nomeSistemaDiNumerazione = 'Binario (Bin)'
elif scelta == 3:
base = 8
nomeSistemaDiNumerazione = 'Ottale (Ott)'
elif scelta == 4:
base = 16
nomeSistemaDiNumerazione = "Esadecimale (Esa)"
if scelta != 5:
# Calcolo i primi 8 pesi in base al sistema di numerazione scelto
print("Pesi delle prime 8 cifre di un numero " + nomeSistemaDiNumerazione)
for x in range(8):
print(str((x + 1)) + ") " + str(int(math.pow(base, x))))
risposta = input("Premi invio per continuare ...")
print("Fine programma")
Laboratorio 2
Creare un programma che converte un numero decimale in un numero:
1) Binario (Bin)
2) Ottale (Ott)
3) Esadecimale (Esa)
Soluzione JavaScript
var input = require("readline-sync");
var numero = 0;
var numeroDecimale = 0;
var numeroConvertito = "";
var base = 0;
var risultato = 0;
var resto = 0;
var cifre = [];
var cifreNumero = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F'];
var nomeSistemaDiNumerazione = "";
var risposta = "";
var scelta = 0;
do {
cifre = [];
numeroDecimale = parseInt(input.question("Inserisci un numero decimale: "))
while (numeroDecimale < 0 || isNaN(numeroDecimale)) {
console.log("Errore: inserire un numero uguale a zero o mmaggiore di zero ...");
numeroDecimale = parseInt(input.question("Inserisci un numero decimale: "))
}
// Menu per la scelta del sistema di numerazione
console.log("1) Sistema Binario (Bin)");
console.log("2) Sistema Ottale (Ott)");
console.log("3) Sistema Esadecimale (Esa)");
scelta = parseInt(input.question("Scegli il sistema di converione: "))
// Visualizzo un errore se la scelta non è corretta
while (scelta < 1 || scelta > 3 || isNaN(scelta)) {
console.log("Errore:scegli un numero tra 1 e 3 ...");
scelta = parseInt(input.question("Scegli il sistema di conversione: "));
}
// Imposto la base e il nome del sistema di numerazione scelto
if (scelta == 1) {
base = 2;
nomeSistemaDiNumerazione = "Binario (Bin)";
} else if (scelta == 2) {
base = 8;
nomeSistemaDiNumerazione = "Ottale (Ott)";
} else if (scelta == 3) {
base = 16;
nomeSistemaDiNumerazione = "Esadecimale (Esa)";
}
// Converto il numero decimale nel sistema di numerazione scelto
numero = numeroDecimale;
while (numero >= base) {
risultato = Math.floor(numero / base);
resto = numero % base;
cifre.push(resto);
numero = risultato;
}
cifre.push(numero);
// stampo il numero convertito
numeroConvertito = "";
for (var x = cifre.length - 1; x >= 0; x--) {
numeroConvertito = numeroConvertito + cifreNumero[cifre[x]];
}
console.log("Numero decimale da convertire: " + numeroDecimale);
console.log("Numero convertito in " + nomeSistemaDiNumerazione + " " + numeroConvertito);
risposta = input.question("Vuoi convertire un altro numero (s/n) ? ");
while (risposta.toLowerCase() != 's' && risposta.toLowerCase() != 'n') {
console.log("Errore: inserire s oppure n ...");
risposta = input.question("Vuoi convertire un altro numero (s/n) ? ");
}
} while (risposta.toLowerCase() == 's');
console.log("Fine programma");
Soluzione Python
numero = 0
numeroDecimale = 0
numeroConvertito = ''
base = 0
risultato = 0
resto = 0
cifre = []
cifreNumero = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F']
nomeSistemaDiNumerazione = ''
risposta = 's'
scelta = 0
while risposta=='s':
cifre = []
numeroDecimale = int(input("Inserisci un numero decimale: "))
while numeroDecimale < 0:
print("Errore: inserire un numero uguale a zero o mmaggiore di zero ...")
numeroDecimale = int(input("Inserisci un numero decimale: "))
# Menu per la scelta del sistema di numerazione
print("1) Sistema Binario (Bin)")
print("2) Sistema Ottale (Ott)")
print("3) Sistema Esadecimale (Esa)")
scelta = int(input("Scegli il sistema di converione: "))
# Visualizzo un errore se la scelta non è corretta
while scelta < 1 or scelta > 3:
print("Errore:scegli un numero tra 1 e 3 ...")
scelta = int(input("Scegli il sistema di converione: "))
# Imposto la base e il nome del sistema di numerazione scelto
if scelta == 1:
base = 2
nomeSistemaDiNumerazione = 'Binario (Bin)'
elif scelta == 2:
base = 8
nomeSistemaDiNumerazione = 'Ottale (Ott)'
elif scelta == 3:
base = 16
nomeSistemaDiNumerazione = 'Esadecimale (Esa)'
# Converto il numero decimale nel sistema di numerazione scelto
numero = numeroDecimale
while numero >= base:
risultato = int(numero / base)
resto = numero % base
cifre.append(resto)
numero = risultato
cifre.append(numero)
# stampo il numero convertito
numeroConvertito = ""
for x in range(len(cifre)-1,-1,-1):
numeroConvertito = numeroConvertito + cifreNumero[cifre[x]]
print("Numero decimale da convertire: " + str(numeroDecimale))
print("Numero convertito in " + nomeSistemaDiNumerazione + " " + numeroConvertito)
risposta = input("Vuoi convertire un altro numero (s/n) ? ")
while risposta.lower() != 's' and risposta.lower() != 'n':
print("Errore: inserire s oppure n ...")
risposta = input("Vuoi convertire un altro numero (s/n) ? ")
print("Fine programma")
Come eseguire i programmi JavaScript
Per eseguire i programmi JavaScript, bisogna installare il framework node.js sul proprio computer.
Il download del file d'installazione può essere fatto collegandosi al link: https://nodejs.org/it/download/.
Il file di download deve corrispondere al sistema operativo installato sul proprio computer.
Dopo il download eseguire il file per installare node.js.
Per verificare se il framework node.js è stato installato correttamente, dal prompt dei comandi del sistema operativo usato, eseguire il comando:
node --version
dovrebbe essere visualizzata la versione di node.js installata, come mostra l'immagine seguente:

Successivamente bisogna creare una cartella "laboratori" dove salvare i due programmi JavaScript da eseguire.
Per salvare i programmi nella cartella "laboratori", basta copiarli nel blocco note o in qualunque editor di testo e salvarli con i nomi:
1) calcola_pesi.js
2) converti_decimale.js
Infine, da prompt dei comandi, entrare nella cartella laboratori ed eseguire il comando:
npm install readline-sync
Questa libreria serve per permettere l'inserimento di dati da tastiera, quando vengono eseguiti i programmi.
A queso punto si possono eseguire i programmi con il comando node, che è l'interprete JavaScript di node.js, come mostrano gli esempi seguenti:
node calcola_pesi
oppure
node converti_decimale
Come eseguire i programmi Python
Per eseguire i programmi scritti Python, bisogna installare il framework python sul proprio computer.
Il download del file d'installazione può essere fatto collegandosi al link: https://www.python.org/downloads/.
Il file di download deve corrispondere al sistema operativo installato sul proprio computer.
Dopo il download eseguire il file per installare python.
Attenzione, durante l'installazione è importante spuntare l'opzione "Add Python 3.X to PATH:

Per verificare se il framework python è stato installato correttamente, dal prompt dei comandi del sistema operativo usato, eseguire il comando:
python --version
dovrebbe essere visualizzata la versione di python installata, come mostra l'immagine seguente:

Successivamente bisogna creare una cartella "laboratori" dove salvare i programmi python da eseguire.
Per salvare i programmi nella cartella "laboratori", basta copiarli nel blocco note o in qualunque editor di testo e salvarli con il nomi:
1) calcola_pesi.py
2) converti_decimale.py
Infine, per eseguire i programmi, da prompt dei comandi, entrare nella cartella laboratori ed il comando:
python calcola_pesi.py
oppure
python converti_decimale.py
Leggi anche le altre lezioni ...
COMPETENZE PER PROGRAMMARE:
2-Mondo reale e Mondo Digitale
3-La reppresentazione digitale dei numeri interi e decimali
4-Le stringhe
5-Le espressioni regolari (REGEXP)
6-Date, ore e fusi orari
Segui sul canale YouTube "Skill Factory Channel" la Playlist: COMPETENZE PER PROGRAMMARE
TUTORIALS
1-Laboratori di logica di programmazione in C
2-Impariamo a programmare con JavaScript
3-Ricominciamo dal linguaggio SQL
4-Introduzione alla logica degli oggetti
5-TypeScript
6-Impariamo a programmare in Python
7-Come sviluppare un sito in WordPress
PAR GOL (Garanzia di Occupabilità dei Lavoratori)

Se sei residente in Campania e cerchi lavoro, sai che puoi partecipare gratuitamente ad un corso di formazione professionale PAR GOL?
I corsi di formazione professionale PAR GOL sono finanziati dalla Regione Campania e ti permettono di acquisire una Qualifica Professionale Europea (EQF) e di partecipare ad un tirocinio formativo aziendale.
Invia il tuo CV o una manifestazione d'interesse a: recruiting@skillfactory.it
oppure
chiama ai seguenti numeri di telefono:
Tel.: 081/18181361
Cell.: 327 0870141
oppure
Contattaci attraverso il nostro sito: www.skillfactory.it
Per maggiori informazioni sul progetto PAR GOL, clicca qui.
Per maggiori informazioni sulle Qualifiche Professionali Europee (EQF), clicca qui.
Academy delle professioni digitali
Per consultare il catalogo dei corsi online della nostra Academy ...

... collegati al nostro sito: www.skillfactory.it
Excel delle meraviglie Lezione 10 - Analisi statistica di una popolazione di dati
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 06/04/2021 00:33:27 | in Tutorials
Skill Factory - 06/04/2021 00:33:27 | in Tutorials
In questa lezione utilizzerete le principali funzioni statistiche o di database di Excel per analizzare una popolazione di dati di un sito che vende prodotti online.
Prima d'iniziare è importante dare una definizione di statistica.
Che cos'è la statistica
La statistica è lo strumento che permette di trasformare le informazioni, organizzate sotto forma di dati, in conoscenza.
 La conoscenza dei dati può essere quantitativa oppure qualitativa. Una ricerca quantitativa richiede una grossa quantità di dati, per ottenere informazioni oggettive sulla cosa che si sta analizzando.
La conoscenza dei dati può essere quantitativa oppure qualitativa. Una ricerca quantitativa richiede una grossa quantità di dati, per ottenere informazioni oggettive sulla cosa che si sta analizzando.
L’analisi qualitativa è una ricerca mirata, che permette di individuare una serie di sfumature di un determinato comportamento o evento che non potrebbero essere colte con un’analisi quantitativa.
La statistica è importante perché ci permette di valutare ciò che osserviamo e di prendere decisioni, è descrittiva se si limita a descrivere i fenomeni attraverso indici e grafici, è inferenziale se si avvale di metodi probabilistici, per trarre conclusioni generali a partire dall'esame di un campione.
La statistica inferenziale non ci dice mai se una cosa è vera o falsa, ma ci permette di determinare la probabilità per stabilire se una cosa può essere vera o falsa.
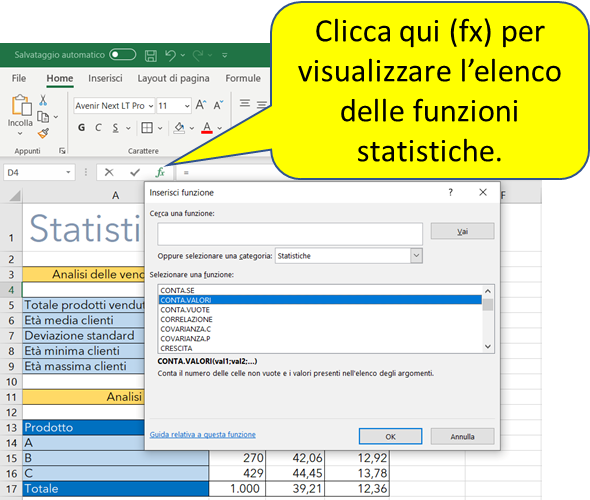
Principali funzioni di Excel per fare statistica
In Excel per fare statistica potete utilizzare le funzioni statistiche e di database, per ottenere l'elenco completo di queste funzioni cliccate sull'icona fx e selezionate le categorie statistiche oppure database, come mostra l'immagine seguente:
Obiettivo della nostra analisi statistica
La nostra analisi statistica prevede lo studio della popolazione di dati inserita nel foglio Excel "Prodotti acquistati online":
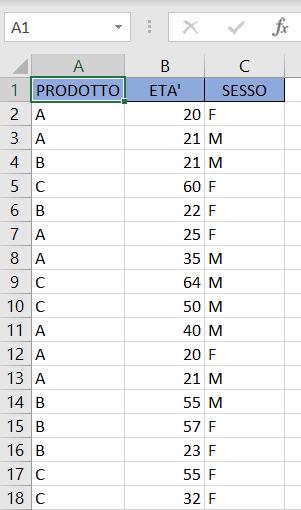
i dati sono stati estratti da un sito e-commerce che vende prodotti online. L'obiettivo è quello di capire quali e quanti prodotti sono stati venduti e l'età media dei clienti, sia per sesso, sia per fasce di età.
L'attività di analisi verrà gestita attraverso diversi livelli di approfondimento, per ottenere informazioni sempre più dettagliate.
Per calcolare l'età media dei clienti, in base al livello di dettaglio, utilizzerete sia la media aritmetica, sia la media ponderata, di seguito trovate le informazioni che vi servono per capire come calcolare questi due tipi di misure.
Media aritmetica
La media aritmetica serve per sintetizzare una distribuzione di valori attraverso un numero che ne rappresenta la sintesi, quindi si può considerare un indicatore di sintesi di una distribuzione di valori.
Per calcolare la media aritmetica di n numeri, si applica la formula seguente:
Xm=(X1+X2+X3+...+Xn)/n
in Excel potete usare la funzione:
=media(intervallo_di_valori)
Per capire quanto è affidabile la media aritmetica, dovete calcolare o la varianza oppure la deviazione standard.
Varianza e deviazione standard
La varianza si calcola con la formula seguente:
Varianza=(X1-Xm)^2+(X2-Xm)^2+(X3-Xm)^2+...+(Xn-Xm)^2
in Excel potete usare la funzione:
=var(intervallo_di_valori)
Questa formula permette di misurare la variabilità di una distribuzione di dati.
Giacché la varianza, per evitare i valori negativi, è espressa al quadrato, per indicare l'affidabilità della media conviene usare la deviazione standard o scarto quadratico medio, che corrisponde alla radice quadrata della varianza e quindi è una grandezza della stessa dimensione della media aritmetica, in Excel potete usare la funzione:
=dev.st(intervallo_di_valori)
Media ponderata o pesata
Per calcolare la media ponderata servono le seguenti informazioni:
1) le osservazioni o classi;
2) i pesi;
3) la numerosità totale.
Facciamo un esempio:
per calcolare la media ponderata delle età dei clienti che hanno acquistato un particolare prodotto online, dovete prima di tutto indicare le classi di età (osservazioni) a cui siete interessati:
18-25
26-35
36-50
51-65
Successivamente, per ogni classe (osservazioni), dovete calcolare il numero di clienti che hanno acquistato un prodotto online (pesi):
18-25 10
26-35 15
36-50 10
51-65 5
Infine, il rapporto tra i clienti di ogni classe ed i clienti totali (numerosità totale), vi permette di calcolare la media ponderata distribuita par ogni classe:
18-25 10 25% (10/40)*100
26-35 15 37,5% (15/40)*100
36-50 10 25% (10/40)*100
51-65 5 12,5% (5/40)*100
---------------------------------
Totale 40 100%
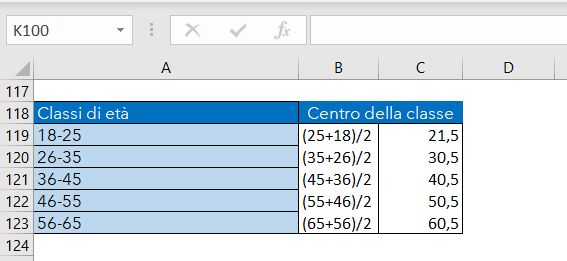
Le classi permettono anche di calcolare l'età media per ogni intervallo di età scelto, per ottenere questo risultato dovete calcolare il valore centrale delle classi, come indicato nell'esempio seguente:
(25+18)/2=21,5
(35+26)/2=30,5
(50+36)/2=43
(65+51)/2=58
A questo punto potete iniziare ad analizzare la popolazione dei dati del sito e-commerce.
Analisi della popolazione di dati del sito e-commerce (primo livello)
In questo primo livello analizzerete la popolazione di dati disponibile per conoscere: la quantità di prodotti venduti, l'età media, l'età minima e l'età massima dei clienti.
Per ottenere queste informazioni dovete utilizzare le seguenti funzioni di Excel:
=CONTA.VALORI('Prodotti acquistati online'!$A$2:$A$1001)
=MEDIA('Prodotti acquistati online'!$B$2:$B$1001)
=MIN('Prodotti acquistati online'!$B$2:$B$1001)
=MAX('Prodotti acquistati online'!$B$2:$B$1001)
Per indicare il livello di affidabilità dell'età media dei clienti che acquistano i prodotti online, dovete calcolare la deviazione standard, utilizzando la funzione di Excel:
DEV.ST('Prodotti acquistati online'!$B$2:$B$1001)
Di seguito la tabella con i dati richiesti:
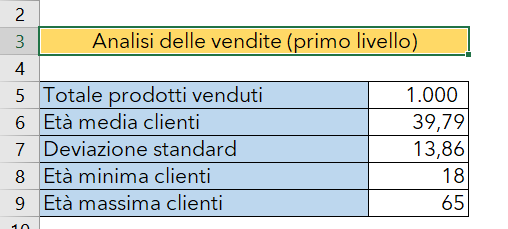
La deviazione standard è molto alta, quindi l'età media dei clienti che acquistano prodotti online non è sicuramente soggetta a grosse variazioni, nell'intervallo di età tra i 18 ed i 65 anni.
Analisi della popolazione di dati del sito e-commerce (secondo livello)
Per proseguire con un'analisi più approfondita dei dati disponibili, dovete conoscere prima quali sono i prodotti venduti. Per ottenere questo risultato dovete estrarre i prodotti venduti dalla popolazione di dati ed eliminare i duplicati, eseguendo le operazioni seguenti:
1) Nel foglio in cui è presente la popolazione di dati che state analizzando, copiate ed incollate in E1 e in G1 il titolo della colonna prodotto e nella cella E2 inserite un asterisco per indicare che volete estrarre dall'elenco tutti i prodotti, come mostra l'immagine seguente:
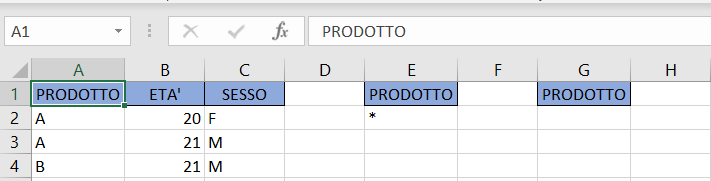
Successivamente selezionate Dati, filtri avanzate e compilate la scheda filtro avanzato come indicato nell'immagine seguente:
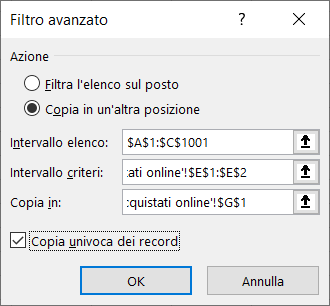
Cliccando sul pulsante ok, otterrete l'elenco dei prodotti venduti, senza duplicati.
A questo punto potete calcolare: la quantità venduta, l'età media dei clienti, la deviazione standard, l'età minima e l'età massima di ogni singolo prodotto, utilizzando le funzioni seguenti:
=CONTA.SE('Prodotti acquistati online'!$A$2:$A$1001;Statistiche!A14)
=CONTA.SE('Prodotti acquistati online'!$A$2:$A$1001;Statistiche!A15)
=CONTA.SE('Prodotti acquistati online'!$A$2:$A$1001;Statistiche!A16)
=MEDIA.SE('Prodotti acquistati online'!A2:A1001;Statistiche!A14;'Prodotti acquistati online'!B2:B1001)
=MEDIA.SE('Prodotti acquistati online'!A2:A1001;Statistiche!A15;'Prodotti acquistati online'!B2:B1001)
=MEDIA.SE('Prodotti acquistati online'!A2:A1001;Statistiche!A17;'Prodotti acquistati online'!B2:B1001)
=DB.DEV.ST(db;'Prodotti acquistati online'!$B$1;Criteri!A2:A3)
=DB.DEV.ST(db;'Prodotti acquistati online'!$B$1;Criteri!A4:A5)
=DB.DEV.ST(db;'Prodotti acquistati online'!$B$1;Criteri!A6:A7)
=DB.MIN(db;'Prodotti acquistati online'!$B$1;Criteri!$A$2:$A$3)
=DB.MIN(db;'Prodotti acquistati online'!$B$1;Criteri!$A$8:$A$9)
=DB.MIN(db;'Prodotti acquistati online'!$B$1;Criteri!$A$10:$A$11)
=DB.MAX(db;'Prodotti acquistati online'!$B$1;Criteri!$A$2:$A$3)
=DB.MAX(db;'Prodotti acquistati online'!$B$1;Criteri!$A$8:$A$9)
=DB.MAX(db;'Prodotti acquistati online'!$B$1;Criteri!$A$10:$A$11)
L'immagine seguente mostra l'area dei criteri utilizzati nelle funzioni DB:
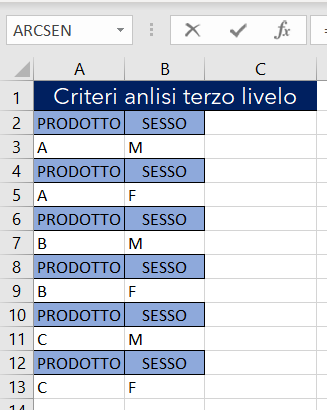
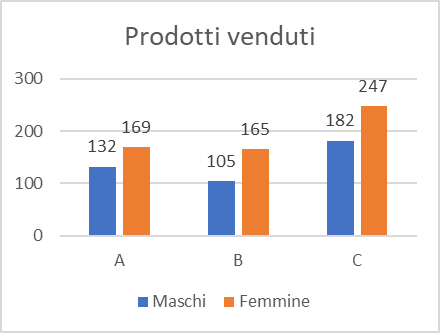
L'immagine seguente mostra la tabella ed i grafici con i risultati dei calcoli:
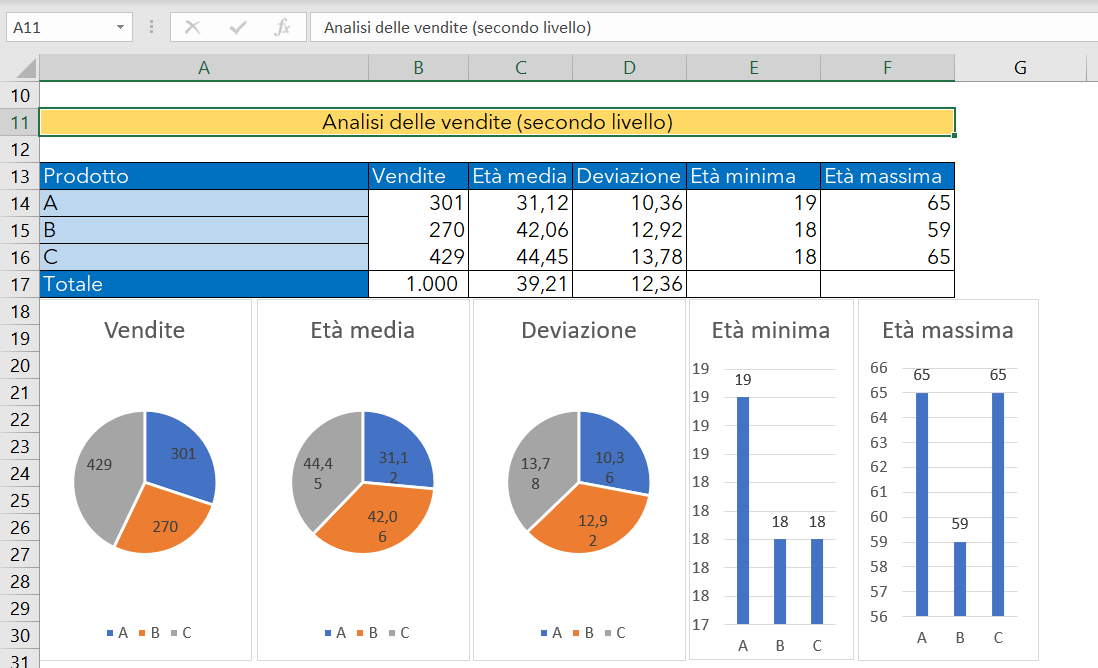
Per creare i grafici, basta selezionare con il mouse la colonna prodotti da A13:A16, e successivamente, tenendo premuto il tasto ctrl, selezionate la colonna con i dati da associare al grafico. Con la selezione attiva, cliccate sul menu inserisci e scegliete il tipo di grafico da creare, come mostra l'immagine seguente:
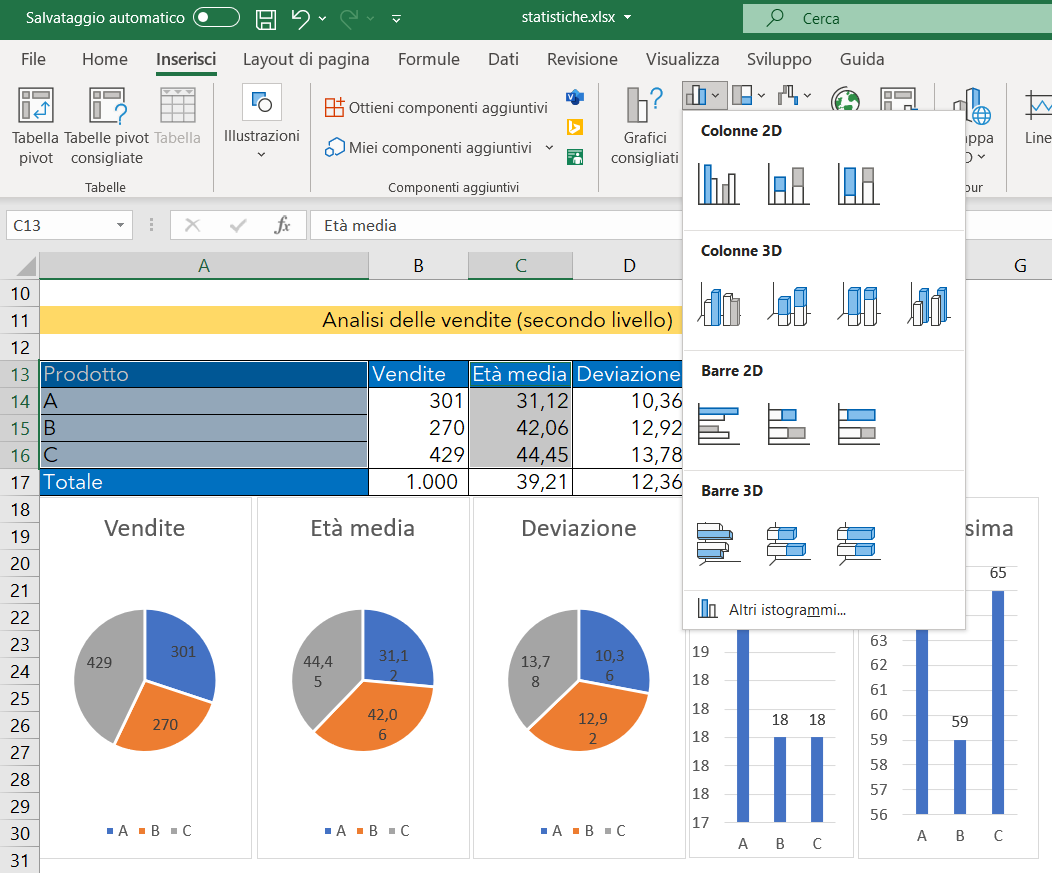
Analisi della popolazione di dati del sito e-commerce (terzo livello)
Adesso potete dettagliare ulteriormente i dati del livello precedente, introducendo una nuova variabile di selezione, il sesso.
Per ottenere questo risultato dovete usare le funzioni seguenti:
Maschi
=DB.CONTA.VALORI(db;'Prodotti acquistati online'!$A$1;Criteri!A2:B4)
=DB.CONTA.VALORI(db;'Prodotti acquistati online'!$A$1;Criteri!A6:B7)
=DB.CONTA.VALORI(db;'Prodotti acquistati online'!$A$1;Criteri!A10:B11)
=DB.MEDIA(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$2:$B$3)
=DB.MEDIA(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$6:$B$7)
=DB.MEDIA(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$10:$B$11)
=DB.DEV.ST(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$2:$B$3)
=DB.DEV.ST(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$6:$B$7)
=DB.DEV.ST(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$10:$B$11)
=DB.MIN(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$2:$B$3)
=DB.MIN(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$6:$B$7)
=DB.MIN(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$10:$B$11)
=DB.MAX(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$2:$B$3)
=DB.MAX(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$6:$B$7)
=DB.MAX(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$10:$B$11)
Femmine
=DB.CONTA.VALORI(db;'Prodotti acquistati online'!$A$1;Criteri!A4:B5)
=DB.CONTA.VALORI(db;'Prodotti acquistati online'!$A$1;Criteri!A8:B9)
=DB.CONTA.VALORI(db;'Prodotti acquistati online'!$A$1;Criteri!A12:B13)
=DB.MEDIA(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$4:$B$5)
=DB.MEDIA(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$8:$B$9)
=DB.MEDIA(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$12:$B$13)
=DB.DEV.ST(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$4:$B$5)
=DB.DEV.ST(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$8:$B$9)
=DB.DEV.ST(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$12:$B$13)
=DB.MIN(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$4:$B$5)
=DB.MIN(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$8:$B$9)
=DB.MIN(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$12:$B$13)
=DB.MAX(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$4:$B$5)
=DB.MAX(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$8:$B$9)
=DB.MAX(statistiche.xlsx!db;'Prodotti acquistati online'!$B$1;Criteri!$A$12:$B$13)
L'immagine seguente mostra l'area dei criteri utilizzati nelle funzioni:

L'immagine seguente mostra le tabelle ed i grafici con i risultati dei calcoli:
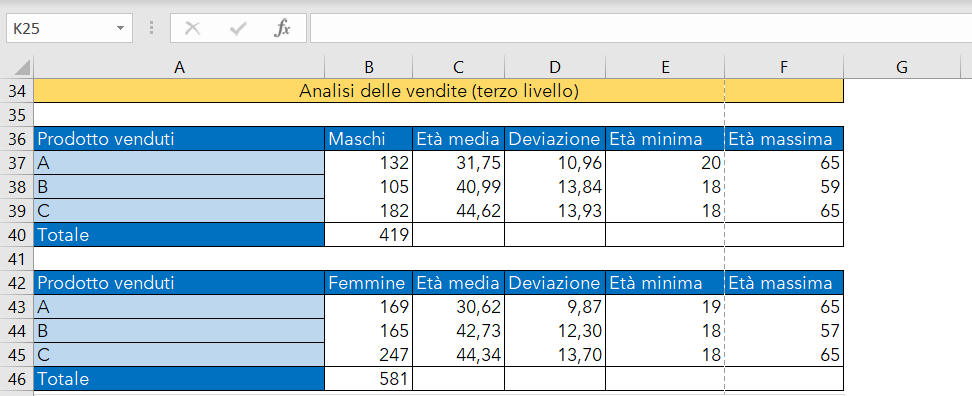
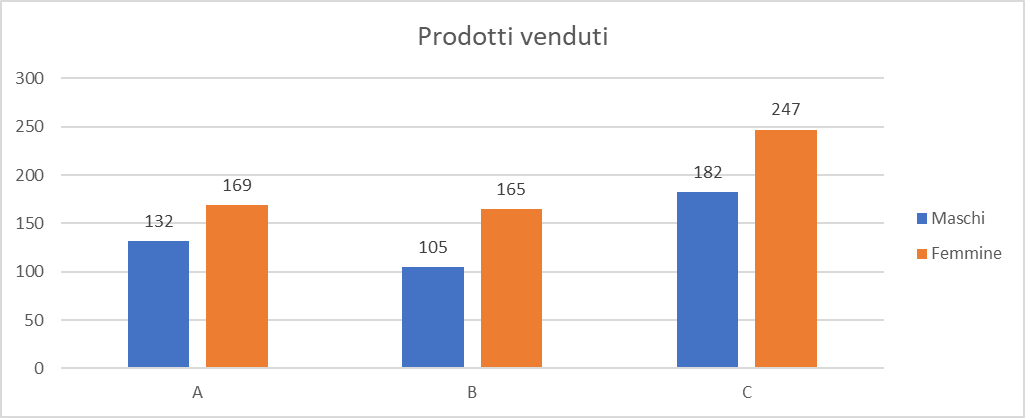
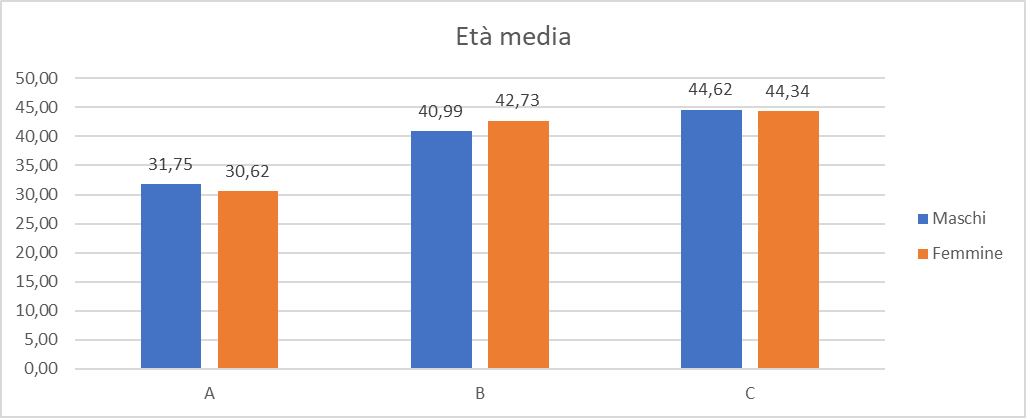
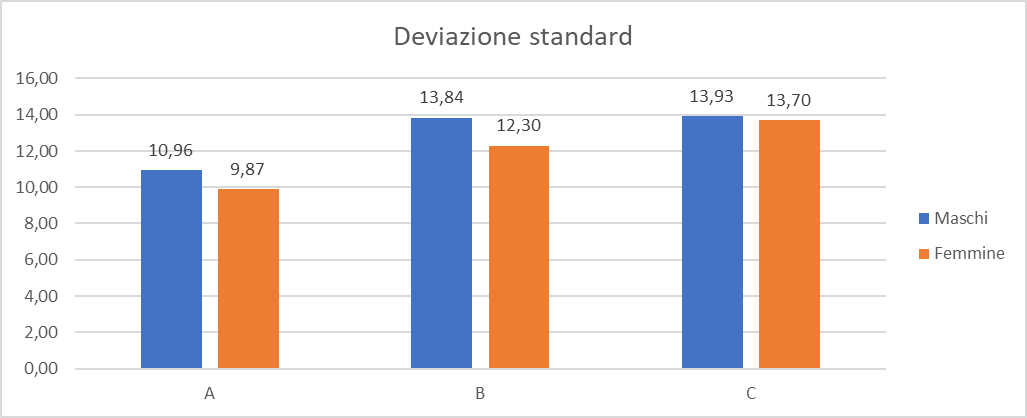
Come creare istogrammi che permettono di confrontare due serie di dati
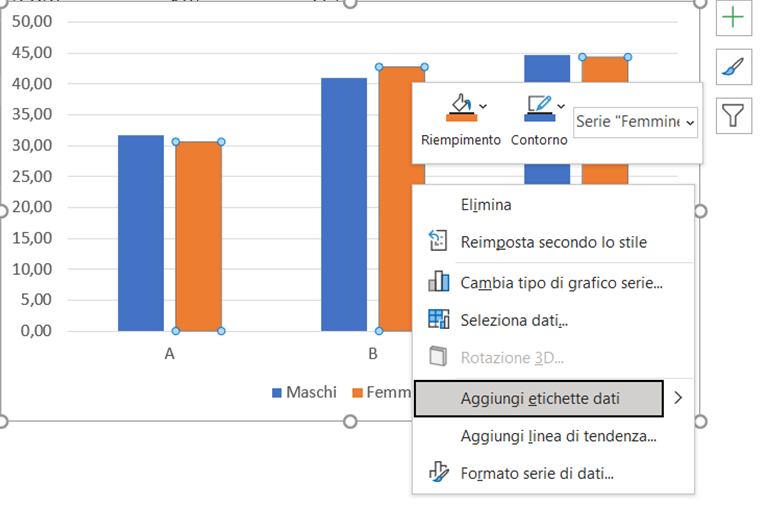
Per creare un istogramma che permette di confrontare due serie di dati, cliccate su inserisci e selezionate un grafico di tipo istogramma.
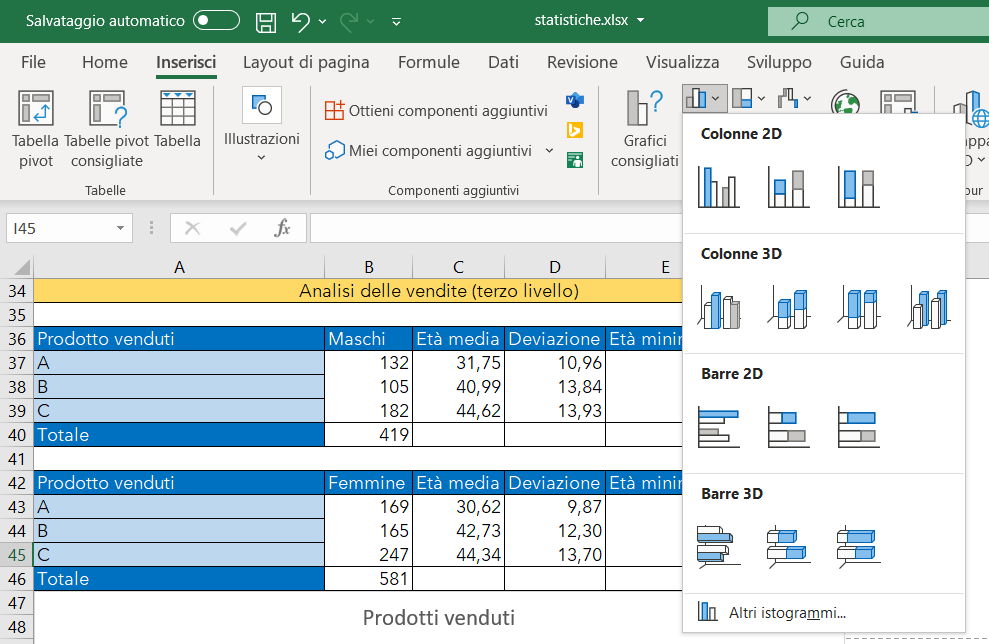
Successivamente selezionate il grafico aggiunto al foglio di lavoro, premete il pulsante destro del mouse e quando appare il menu selezionate il comando Seleziona dati ...
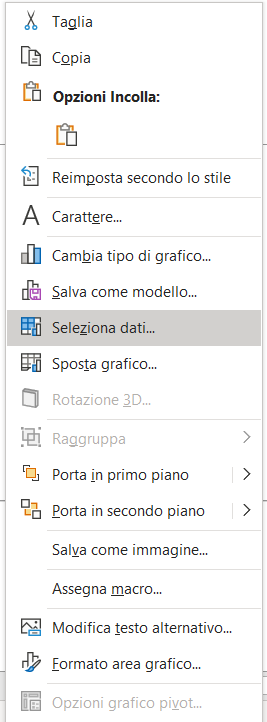
Nella scheda seleziona origine dati rimuovete eventuali informazioni presenti e cliccate sul pulsante aggiungi, per selezionare la prima serie di dati.
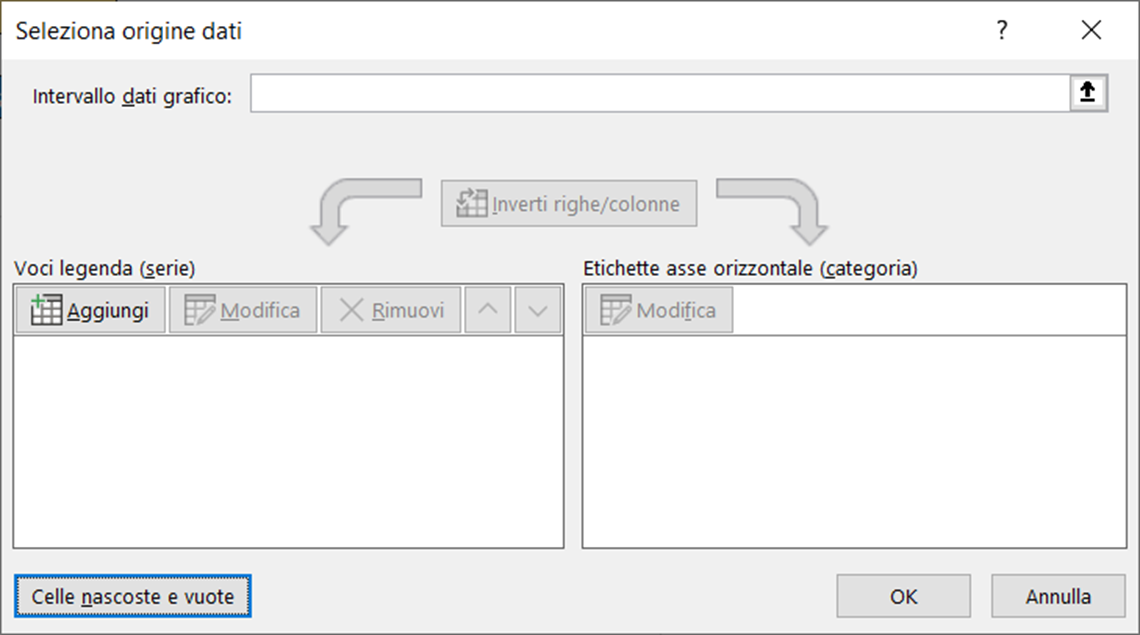
Selezionate il nome da assegnare alla prima serie, poi selezionate i valori corrispondenti ed infine confermate con ok.
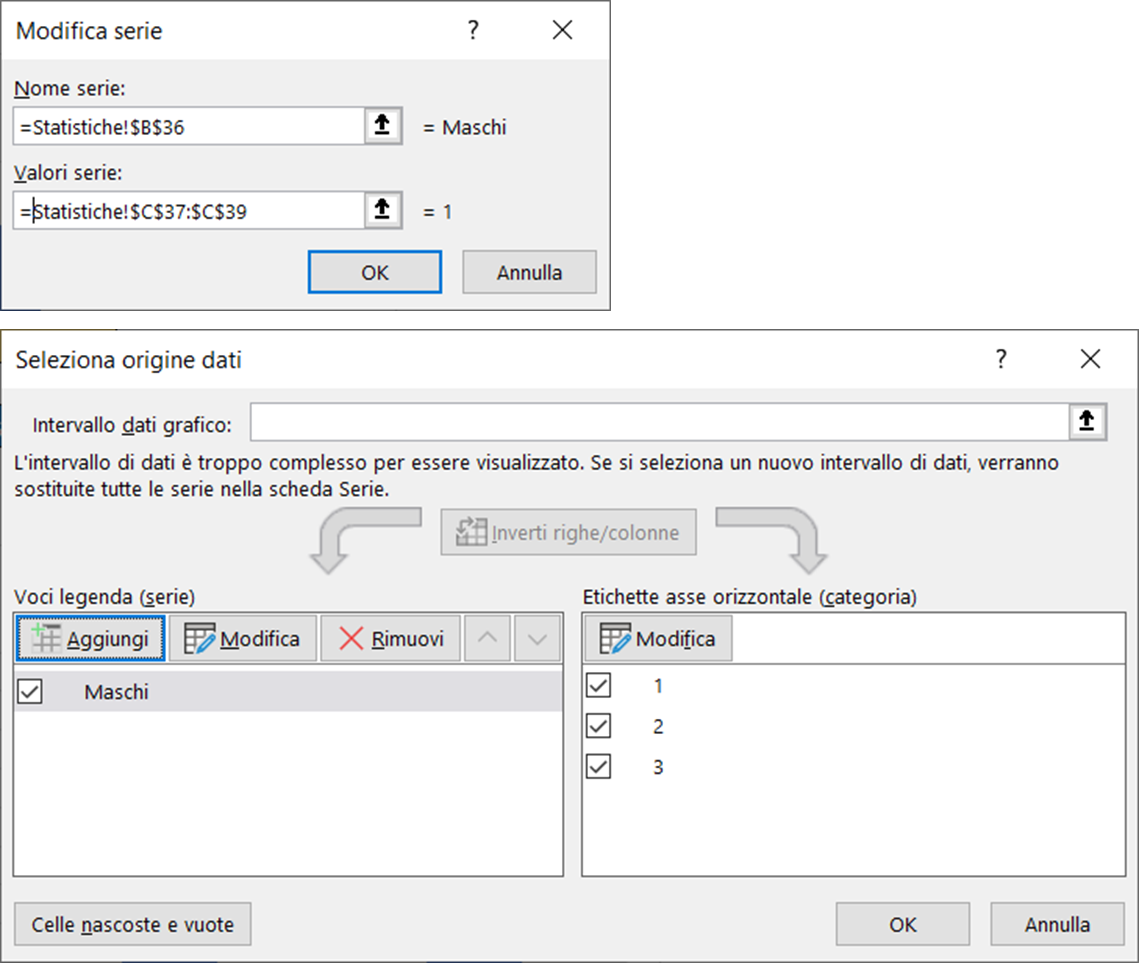
Ripetete le stesse operazioni per aggiungere la seconda serie.
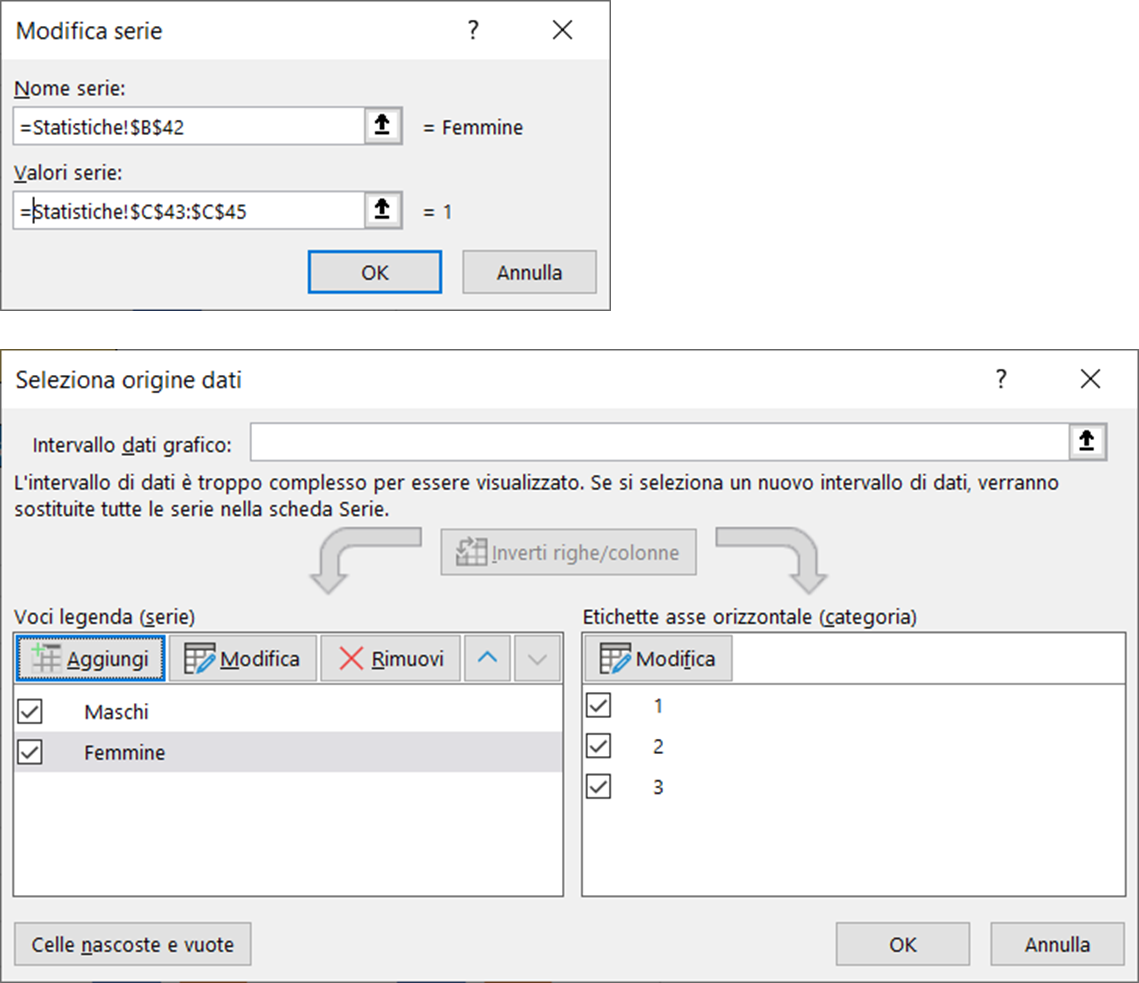
Per completare, cliccate sul pulsante modifica, e selezionate le etichette da associare alle serie di dati.
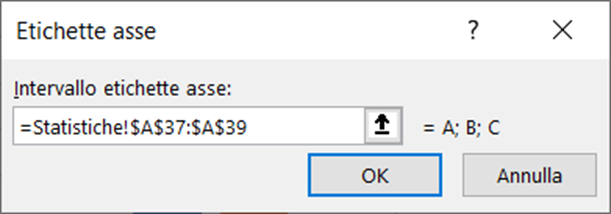
Per visualizzare le etichette dati sulle barre del grafico, selezionate un gruppo di barre, premete il pulsante destro del mouse e dal menu selezionate il comando Aggiungi etichette dati.
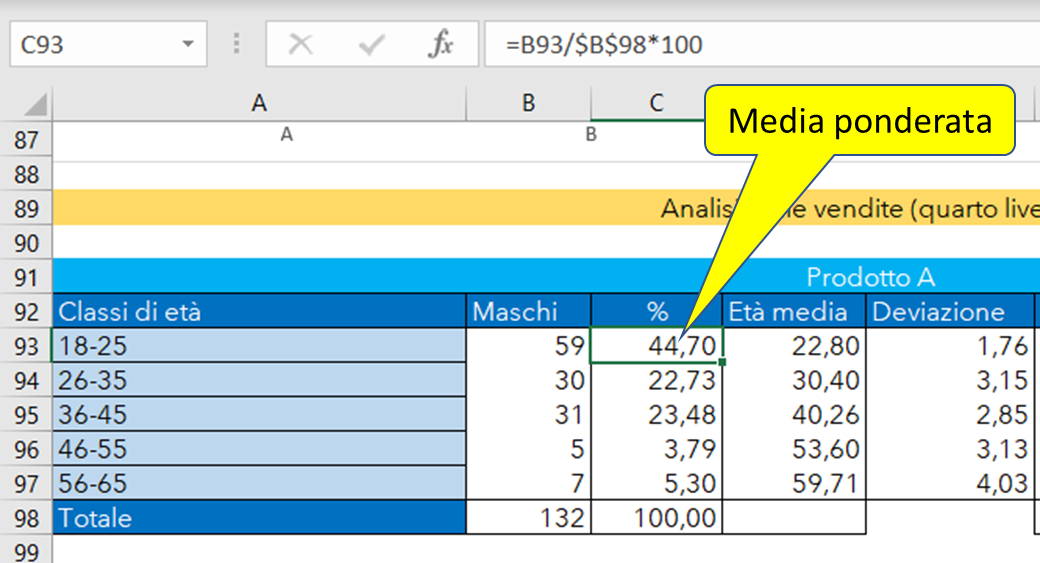
Analisi della popolazione di dati del sito e-commerce (quarto livello)
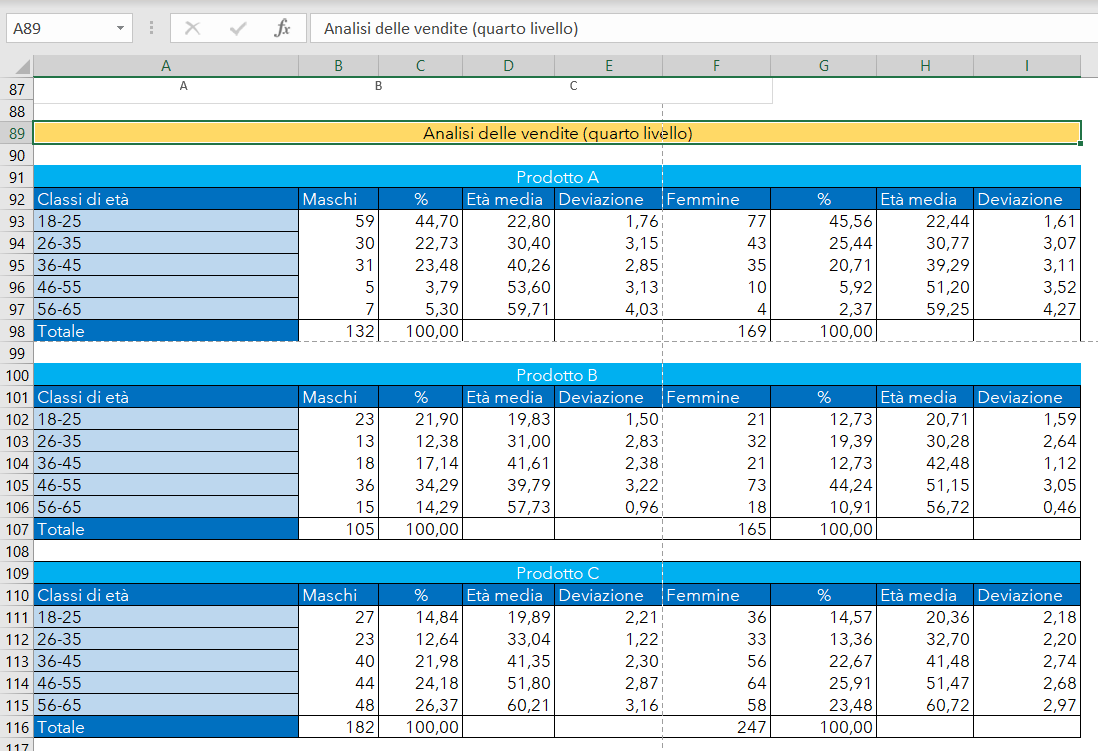
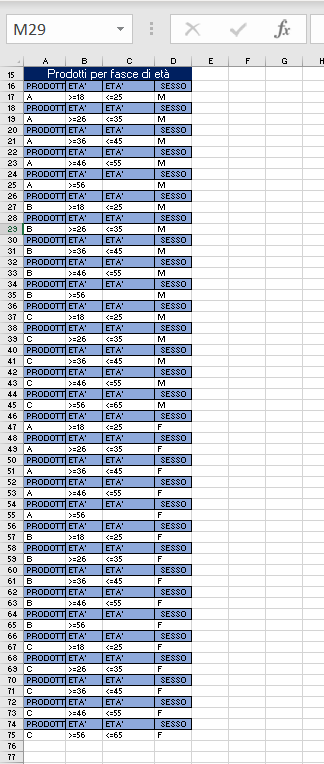
=DB.CONTA.VALORI(db;'Prodotti acquistati online'!$A$1;Criteri!$A$16:$D$17)
=DB.MEDIA(db;'Prodotti acquistati online'!$B$1;Criteri!$A$16:$D$17)
=DB.DEV.ST(db;'Prodotti acquistati online'!$B$1;Criteri!$A$16:$D$17)
<< Lezione precedente | Lezione successiva >>
T U T O R I A L S S U G G E R I T I
- Impariamo Python giocando al "Solitario del ferroviere"
- Impariamo a programmare con JavaScript
- Laboratori di Logica di programmazione in C
- Introduzione alla Logica degli oggetti
- Ricominciamo ... dal Linguaggio SQL
- APP Mania
- Come sviluppare un Sito con Wordpress
EDUCATIONAL GAMING BOOK (EGB) "H2O"
 Nell'era dello SMART LEARNING e di PYTHON i libri non si scrivono, ma si sviluppano, in questo modo chi studia, può sperimentare ed apprendere contemporaneamente; un libro con queste caratteristiche lo possiamo definire un Educational Gaming Book (EGB).
Nell'era dello SMART LEARNING e di PYTHON i libri non si scrivono, ma si sviluppano, in questo modo chi studia, può sperimentare ed apprendere contemporaneamente; un libro con queste caratteristiche lo possiamo definire un Educational Gaming Book (EGB).
"H2O" è un EGB che descrive tutte le caratteristiche dell'acqua, la sostanza formata da molecole di H2O, che attraverso il suo ciclo di vita garantisce la sopravvivenza di tutti gli esseri viventi del Pianeta.
L'obiettivo dell'EGB è quello di far conoscere ai giovani le proprietà dell'acqua, sotto molti aspetti uniche, per sensibilizzarli a salvaguardare un bene comune e raro, indispensabile per la vita.
Per il DOWNLOAD di "H2O" clicca qui.
La geometria della tartaruga: "I Quadrilateri" - Lezione 2
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 20/03/2021 18:51:05 | in Tutorials
Skill Factory - 20/03/2021 18:51:05 | in Tutorials
Benvenuti alla seconda lezione di INFORMATEMATICA, l'argomento di questa nuova lezione sono i quadrilateri. Con l'aiuto della tartaruga Pitagora imparerete a disegnare quadrati, rombi, rettangoli e trapezi e a calcolare le loro principali informazioni geometriche.

Per iniziare dovete creare il pannello di controllo dove inserire le informazioni che servono alla tartaruga Pitagora per disegnare il tipo di quadrilatero scelto.
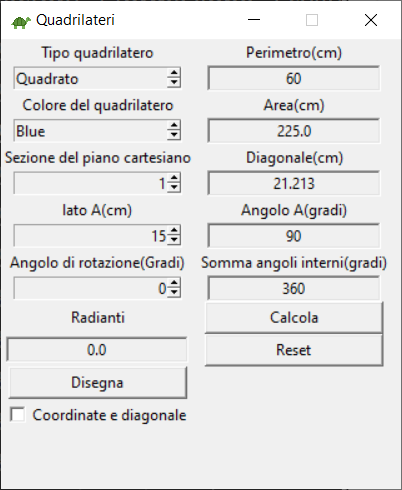
COME CREARE IL PANNELLO DI CONTROLLO PER DISEGNARE I QUATRILATERI
Per creare un'interfaccia grafica con Python dovete importare la libreria Tkinter con il comando seguente:
import tkinter as tk
Potete utilizzare l'alias tk per usare tutti i widget e le funzioni contenute all'interno di questa potente libreria grafica.
I widget più utilizzati sono: Label, Entry, Radiobutton, Checkbutton, Spinbox, Listbox, Button.
Per creare il pannello di controllo che servirà per disegnare i quadrilateri, utilizzeremo i seguenti widget: Label, Spinbox, Checkbutton, Button.
Potete creare la finestra che conterrà i widget con il comando seguente:
root = tk.Tk()
Ad esempio, il codice Python seguente vi permette di creare una finestra, larga 320 pixel ed alta 360 pixel, di disattivare il suo ridimensionamento ed impostare il titolo che apparirà in alto a sinistra:
root = tk.Tk()
root.geometry("320x360")
root.resizable(False,False)
root.title("Quadrilateri")
COME AGGIUNGERE I WIDGET ALLA FINESTRA TKINTER
Dopo la creazione della finestra tkinter, per aggiungere i widget che servono, li dovete prima creare e poi successivamente con le funzioni pack() oppure grid() li potete collegare.
La funzione pack() dispone i componenti in modo sequenziale, dall'alto verso il basso, permettendo di allinearli in alto, in basso, a sinistra e a destra, aggiungendo l'argomento side, come mostra l'esempio seguente:
root = Tk()
root.geometry('250x150')
button1 = Button(text="Left")
button1.pack(side = LEFT)
button2 = Button(text="Top")
button2.pack(side = TOP)
button3 = Button(text="Right")
button3.pack(side = RIGHT)
button4 = Button(text="Bottom")
button4.pack(side = BOTTOM)
root.mainloop()
La funzione grid() permette di disporre i componenti all'interno di una griglia, indicando la loro posizione attraverso la riga e la colonna.
L'esempio seguente mostra come potete aggiungere alla finestra root alcuni dei widget che vi servono:
root = tk.Tk()
root.geometry("320x360")
root.resizable(False,False)
root.title("Quadrilateri")
varTipo=tk.StringVar(root)
colore=tk.StringVar(root)
chkbt=tk.IntVar(root)
lbl_tipo=tk.Label(root,text="Tipo quadrilatero")
tipo=tk.Spinbox(root, values=["Quadrato", "Rombo", "Rettangolo", "Trapezio"], textvariable=varTipo, command=lambda: abilita_disabilita_controlli_pannello_quadrilateri(controlli_a,controlli_b), state="readonly")
lbl_colore=tk.Label(root,text="Colore del quadrilatero")
colore=tk.Spinbox(root,values=("None", "Blue", "Red", "Orange", "Green", "Yellow", "Violet", "Fuchsia", "Pink", "Deepskyblue", "Aqua", "Lightgreen", "Gold", "Peru", "Black", "Gray", "White"], textvariable=colore, state="readonly")
...
disegna = tk.Button(root, width=19, text ="Disegna", command = lambda:disegna_quadrilatero(varTipo.get(), int(rotazione.get()), int(lato_A.get()), int(lato_B.get()),colore.get(), int(sezione.get()), chkbt.get()))
coord_diag = tk.Checkbutton(root, text='Coordinate e diagonale',variable=chkbt,onvalue=1,offvalue=0)
...
lbl_tipo.grid(row=0,column=0)
tipo.grid(row=1,column=0)
lbl_colore.grid(row=2,column=0)
colore.grid(row=3,column=0)
disegna.grid(row=12,column=0)
coord_diag.grid(row=13,column=0)
...
root.mainloop()
Il comando root.mainloop() visualizza il pannello di controllo è si mette in ascolto degli eventi prodotti dagli utenti che usano l'interfaccia grafica.
Principalmente le azioni di un utente che sono associate ad un evento sono due: il click del mouse su un pulsante ed il cambiamento del contenuto di un widget, entrambi gli eventi possono essere associati all'esecuzione di una funzione con l'opzione command, come mostra il codice seguente:
disegna = tk.Button(root, width=19, text ="Disegna", command = lambda:disegna_quadrilatero(tipo.get(),int(rotazione.get()),int(lato_A.get()),int(lato_B.get()),colore.get(),int(sezione.get()),chkbt.get())),
quando l'utente clicca sul button disegna viene eseguita la funzione disegna_quadrilatero(...).
COME GESTIRE I VALORI ASSEGNATI AI WIDGET
Per gestire i valori contenuti nei widget di tipo input come ad esempio: Entry, Radiobutton, Checkbutton, Spinbox, Listbox, dovete associare il componente ad una variabile attraverso le opzioni textvariable o variable, come mostrano gli esempi seguenti:
Esempio 1
varTipo=tk.StringVar(root)
tipo=tk.Spinbox(root, values=["Quadrato", "Rombo", "Rettangolo", "Trapezio"], textvariable=varTipo, command=lambda: abilita_disabilita_controlli_pannello_quadrilateri(controlli_a,controlli_b), state="readonly")
Esempio 2
chkbt=tk.IntVar(root)
coord_diag = tk.Checkbutton(root, text='Coordinate e diagonale',variable=chkbt,onvalue=1,offvalue=0)
Le variabili varTipo e chkbt attraverso le opzioni textvariable e variable sono state associate ai widget tipo e coord_diag, in questo modo attraverso le due variabili potete leggere o assegnare un valore ai due componenti.
Per assegnare o leggere il valore di una variabile associata ad un widget dovete utilizzare le funzioni: set(valore) e get():
print(chkbt.get())
varTipo.set("Quadrato")
COME ELIMINARE UN WIDGET DA UNA FINESTRA TKINTER
Per eliminare un widget da una finestra Tkinter, dovete utilizzare la funzione pack_forget() se il componente è stato collegato con la funzione pack(), altrimenti dovete usare la funzione grid_forget(), come mostra l'esempio seguente:
tipo.grid_forget()
disegna.grid_forget()
Per eliminare velocemente tutti i widget di una finestra, potete aggiungere i loro indirizzi ad una lista ed utilizzare un ciclo for per eliminarli tutti con le funzioni grid_forget() oppure pack_forget(), come mostra la funzione seguente:
#Elimina controlli pannello quadrilateri
def elimina_controlli_pannello_quadrilateri(controlli_a,controlli_b):
for i in range(len(controlli_a)):
controlli_a[i].grid_forget()
for i in range(len(controlli_b)):
controlli_b[i].grid_forget()
Le liste controlli_a e controlli_b contengono i riferimenti a tutti i widget del pannello di controllo usato per gestire i quadrilateri:
lbl_tipo.grid(row=0,column=0)
controlli_a.append(lbl_tipo)
tipo.grid(row=1,column=0)
controlli_a.append(tipo)
lbl_colore.grid(row=2,column=0)
controlli_a.append(lbl_colore)
colore.grid(row=3,column=0)
controlli_a.append(colore)
lbl_sezione.grid(row=4,column=0)
controlli_a.append(lbl_sezione)
sezione.grid(row=5,column=0)
controlli_a.append(sezione)
lbl_lato_A.grid(row=6,column=0)
controlli_a.append(lbl_lato_A)
lato_A.grid(row=7,column=0)
controlli_a.append(lato_A)
LA GEOMETRIA DEL QUADRATO E DEL ROMBO
Il quadrato ed il rombo hanno le stesse caratteristiche geometriche, l'unica differenza è che il rombo ha un angolo di rotazione iniziale di 45 gradi.
Per disegnare entrambe le figure basta un solo lato:
La diagonale di queste due figure geometriche si può calcolare applicando il teorema di pitagora.
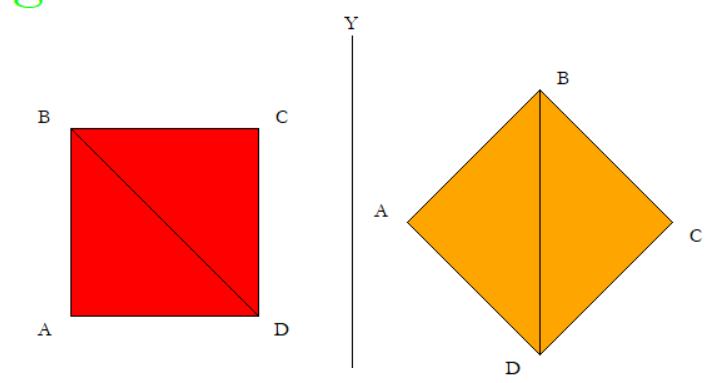
Il codice Python seguente mostra come calcolare la diagonale, il perimetro e l'area, sia del quadrato, sia del rombo:
#Importare la libreria math
import math
#Diagonale
d=round(math.sqrt(math.pow(lato_A,2)+math.pow(lato_A,2)),3)
#Perimetro
p=lato_A*4
#Area
a=math.pow(lato_A,2)
Il codice Python seguente mostra come aggiornare i dati dei widget, nel pannello di controllo:
#Visualizzazione delle informazioni geometriche calcolate nel pannello di controllo
perimetro.config(text=str(p))
area.config(text=str(a))
diagonale.config(text=str(d))
L'angolo alfa adiacente al vertice A, come mostra l'immagine, misura 90°:
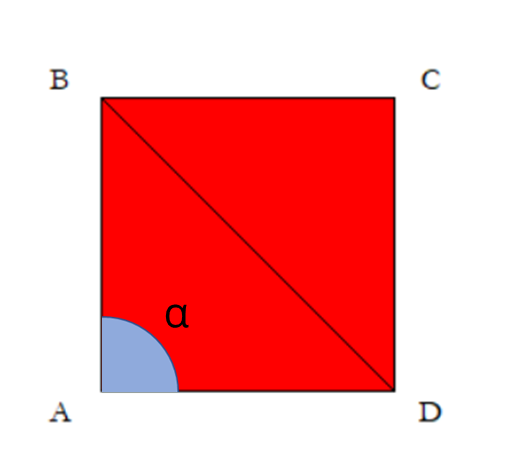
quindi la somma degli angoli interni del quadrato e del rombo corrisponde 360°.
#Angolo adiacente al vertice A
val_angolo_A=90
#Calcolo della somma degli angoli interni del quadrato e del rombo
val_angoli_somma=4*val_angolo_A
#Visualizzazione delle informazioni geometriche calcolate nel pannello di controllo
angolo_A.config(text=str(val_angolo_A))
angoli_somma.config(text=str(val_angoli_somma))
LA GEOMETRIA DEL RETTTANGOLO
Per disegnare un rettangolo occorrono due lati di lunghezza diversa, vi suggerisco di fare in modo che il lato_A sia quello minore ed il lato_B quello maggiore:

Anche in questo caso per calcolare la diagonale del rettangolo si può usare il teorema di pitagora.
Il codice Python seguente mostra come calcolare la diagonale, il perimetro e l'area, del rettangolo:
#Importare la libreria math
import math
#Diagonale
d=round(math.sqrt(math.pow(lato_A,2)+math.pow(lato_B,2)),3)
#Perimetro
p=(lato_A*2)+(lato_B*2)
#Area
a=lato_A*lato_B
#Visualizzazione delle informazioni geometriche calcolate nel pannello di controllo
perimetro.config(text=str(p))
area.config(text=str(a))
diagonale.config(text=str(d))
Anche nel rettangolo, l'angolo alfa adiacente al vertice A misura 90°:
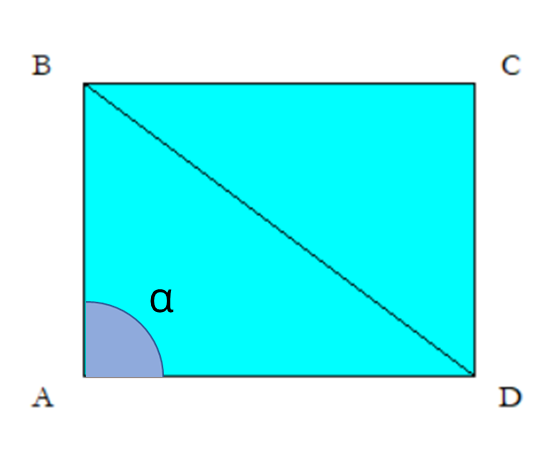
quindi la somma degli angoli interni del quadrato e del rombo corrisponde 360°.
#Angolo adiacente al vertice A
val_angolo_A=90
#Calcolo della somma degli angoli interni del rettangolo
val_angoli_somma=4*val_angolo_A
#Visualizzazione delle informazioni geometriche calcolate nel pannello di controllo
angolo_A.config(text=str(val_angolo_A))
angolo_B.config(text=str(val_angolo_B))
angoli_somma.config(text=str(val_angoli_somma))
LA GEOMETRIA DEL TRAPEZIO
Anche per disegnare un trapezio occorrono due lati di lunghezza diversa, vi suggerisco sempre di fare in modo che il lato_A sia quello minore ed il lato_B quello maggiore:

Il trapezio disegnato dalla tartaruga Pitagora è di tipo isoscele, con due lati obliqui uguali, come mostra l'immagine seguente:
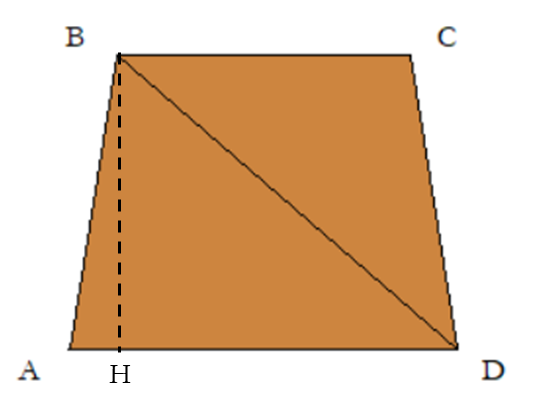
L'altezza BH corrisponde al lato_A, mentre la base HD del triangolo rettangolo bhd corrisponde al lato_A + AH, dove:
AH=(lato_B-lato_A)/2.
Per calcolare la diagonale del trapezio dovete applicare il teorema di pitagora ai cateti BH che corrisponde al lato_A e HD che corrisponde a lato_A+(lato_B-lato_A)/2, come mostra il codice Python seguente:
#Importare la libreria math
import math
#Diagonale
d=round(math.sqrt(math.pow(lato_A,2)+math.pow(lato_A+(lato_B-lato_A)/2,2)),3)
Per calcolare il perimetro del trapezio dovete prima calcolare la dimensione di uno dei lati obliqui, come mostra la formula seguente:
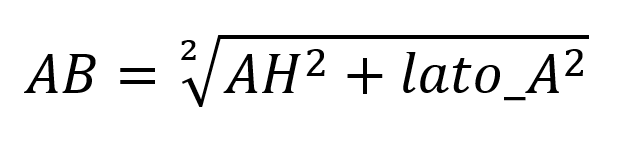
Il codice Python seguente vi permette di calcolare il perimetro del trapezio:
#Calcolo del lato obliquo
lo=round(math.sqrt(math.pow(lato_A,2)+math.pow((lato_B-lato_A)/2,2)),3)
#Perimetro
p=(lo*2)+lato_A+lato_B
Per calcolare l'area del trapezio dovete applicare la formula seguente:
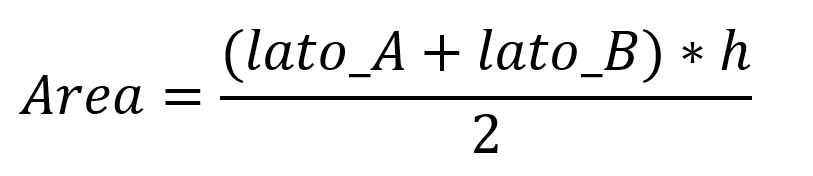
ll codice Python seguente mostra come calcolare l'area del trapezio:
#Area
a=((lato_A+lato_B)*lato_A)/2
Nel trapezio l'angolo alfa adiacente al vertice A è minore di 90° (acutangolo), perché i lati sono obliqui, ma la somma degli angoli interni continua ad essere uguale a 360°.
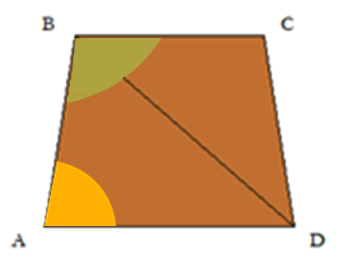
Per calcolare l'angolo alfa adiacente al vertice A dovete procedere come segue:
1) calcolare il seno dell'angolo alfa applicando la formula:
sin=lato_A/lato_Obliquo.
2) successivamente applicando la funzione inversa arcoseno si può ricavare la misura dell'angolo alfa in radianti.
3) per convertire i radianti in gradi applicare la funzione math.degrees(...).
Il codice Python seguente mostra come ottenere la misura espressa in gradi dell'angolo alfa, adiacente ad A:
#Angolo adiacente al vertice A
val_angolo_A=round(math.degrees(math.asin(lato_A/lo)),2)
L'angolo beta, adiacente al vertice B è maggiore di 90° (ottusangolo), per calcolarlo dovete fare due considerazioni:
1) il triangolo ABH è rettangolo, quindi l'angolo corrispondente al vertice H è di 90°.

2) la somma degli angoli interni di un triangolo è uguale a 180°.
Quindi l'angolo beta può essere calcolato come segue:
Angolo_ABH=(180-angolo_alfa-90)
Angolo beta=Angolo_ABH+90=180-angolo_alfa-90+90=180-angolo_alfa.
Il codice Python seguente mostra come ottenere la misura espressa in gradi dell'angolo alfa e dell'angolo beta, in modo da calcolare la somma degli angoli interni del trapezio:
val_angolo_A=round(math.degrees(math.asin(lato_A/lo)),2)
val_angolo_B=round(180-val_angolo_A,2)
val_angoli_somma=2*val_angolo_A+2*val_angolo_B
Usate il codice Python seguente per aggiornare le label della finestra dei quadrilateri:
perimetro.config(text=str(p))
area.config(text=str(a))
diagonale.config(text=str(d))
lato_obliquo.config(text=str(lo))
angolo_A.config(text=str(val_angolo_A))
angolo_B.config(text=str(val_angolo_B))
angoli_somma.config(text=str(val_angoli_somma))

COME DISEGNARE I QUADRILATERI
Per disegnare il quadrilatero scelto dovete prima posizionare la tartaruga Pitagora al centro della sezione del piano cartesiano scelta, la struttura condizionale seguente permette di impostare le coordinate richieste:
#Disegna il quadrilatero al centro del piano cartesiano
if sezione==0:
cx=0
cy=0
#Disegna il quadrilatero in alto a sinistra del piano cartesiano
elif sezione==1:
cx=-150
cy=150
#Disegna il quadrilatero in alto a destra del piano cartesiano
elif sezione==2:
cx=150
cy=150
#Disegna il quadrilatero in basso a sinistra del piano cartesiano
elif sezione==3:
cx=-150
cy=-150
#Disegna il quadrilatero in basso a destra del piano cartesiano
else:
cx=150
cy=-150
Il codice Python seguente permette di posizionare e ruotare la tartaruga Pitagora, prima che inizia a disegnare il quadrilatero:
turtle.goto(cx,cy)
turtle.setheading(270)
turtle.right(rotazione)
Il valore della variabile rotazione, se diverso da zero, permette di ruotare il quadrilatero del numero di gradi indicato, come mostra l'immagine seguente:

Nell'immagine lo stesso quadrato è stato disegnato più volte aggiungendo ogni volta una differenza di rotazione di 15°.
Nel codice Python allegato a questa lezione, nelle funzioni seguenti trovate il codice per disegnare i quadrilateri:
1) def disegna_quadrato_rombo(rotazione,lato_A,colore,sezione,coord_diag)
2) def disegna_rettangolo(rotazione,lato_A,lato_B,colore,sezione,coord_diag)
3) def disegna_trapezio(rotazione,lato_A,lato_B,colore,sezione,coord_diag).
COME DISEGNARE LE DIAGONALI E LE LETTERE DEI VERTICI
Per indicare alla tartaruga Pitagora di disegnare anche la diagonale e le lettere dei vertici dei quadrilateri, dovete selezionare il checbutton coordinate e diagonale.
Per memorizzare le posizioni necessarie per disegnare la diagonale e le lettere dei vertici dei quadrilateri, dovete creare un vettore di oggetti, del tipo seguente:
#Classe per memorizzare le coordinate delle figure geometriche
class MemorizzaCoordinate:
def __init__(self):
self.coordinate = []
def aggiungi(self,coordinata):
self.coordinate.append(coordinata)
def estrai(self):
posizione=self.coordinate[0]
del self.coordinate[0]
return posizione
def resetta(self):
self.coordinate.clear()
L'esempio seguente mostra come utilizzare la classe per memorizzare le posizioni necessarie e disegnare la diagonale e le lettere:
def disegna_rettangolo(rotazione,lato_A,lato_B,colore,sezione,coord_diag):
coordinateDiagonale=MemorizzaCoordinate()
coordinateLettere=MemorizzaCoordinate()
...
for x in range(2):
turtle.right(angoloRotazione)
coordinateLettere.aggiungi(turtle.pos())
turtle.forward(lato_A)
coordinateDiagonale.aggiungi(turtle.pos())
coordinateLettere.aggiungi(turtle.pos())
turtle.right(angoloRotazione)
turtle.forward(lato_B)
if colore!="None":
turtle.color(colore)
turtle.end_fill()
if coord_diag==1:
disegna_diagonale_lettere(cx,cy,coordinateDiagonale,coordinateLettere)
COME INSTALLARE ED ESEGUIRE L'APPLICAZIONE PITAGORA (VERSIONE 2)
Per eseguire l'applicazione Pitagora sul vostro computer, la dovete prima scaricare cliccando qui.
Dopo il download del file pitagora_v2.zip che contiene i file: pitagora_v2.py e tartaruga.png, sul disco c: create la cartella pitagora, ed estraete all'interno i due file.
Per eseguire l'applicazione, da prompt scrivete il comando: python pitagora_v2.py, come mostra l'immagine seguente:
COME INSTALLARE PYTHON
Se non avete installato Python seguite i passaggi seguenti:
1) collegatevi al sito: https://www.python.org;
2) fate il download del file d'installazione;
3) Successivamente per installare Python, eseguite il file python-x.x.x.exe, dove x.x.x. è la versione che state installando;
4) Durante l'installazione non dimenticate di spuntare la selezione:

altrimenti Python si avvierà solo partendo dalla cartella dove verrà installato.
Per far parte della nostra community registrati su www.skillbook.it.
T U T O R I A L S S U G G E R I T I
- TypeScript
- Impariamo Python giocando al "Solitario del ferroviere"
- Impariamo a programmare con JavaScript
- Laboratori di Logica di programmazione in C
- Introduzione alla Logica degli oggetti
- Ricominciamo ... dal Linguaggio SQL
- APP Mania
- Come sviluppare un Sito con Wordpress
- Excel delle meraviglie
EDUCATIONAL GAMING BOOK (EGB) "H2O"
 Nell'era dello SMART LEARNING e di PYTHON i libri non si scrivono, ma si sviluppano, in questo modo chi studia, può sperimentare ed apprendere contemporaneamente; un libro con queste caratteristiche lo possiamo definire un Educational Gaming Book (EGB).
Nell'era dello SMART LEARNING e di PYTHON i libri non si scrivono, ma si sviluppano, in questo modo chi studia, può sperimentare ed apprendere contemporaneamente; un libro con queste caratteristiche lo possiamo definire un Educational Gaming Book (EGB).
"H2O" è un EGB che descrive tutte le caratteristiche dell'acqua, la sostanza formata da molecole di H2O, che attraverso il suo ciclo di vita garantisce la sopravvivenza di tutti gli esseri viventi del Pianeta.
L'obiettivo dell'EGB è quello di far conoscere ai giovani le proprietà dell'acqua, sotto molti aspetti uniche, per sensibilizzarli a salvaguardare un bene comune e raro, indispensabile per la vita.
Per il DOWNLOAD di "H2O" clicca qui.





 Le Tue Aule
Le Tue Aule
 I Tuoi Gruppi
I Tuoi Gruppi
 Le Tue Selezioni
Le Tue Selezioni







