Skill Factory
Lista post > La geometria della tartaruga: "I Quadrilateri" - Lezione 2
La geometria della tartaruga: "I Quadrilateri" - Lezione 2
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 20/03/2021 18:51:05 | in Tutorials
Skill Factory - 20/03/2021 18:51:05 | in Tutorials
Benvenuti alla seconda lezione di INFORMATEMATICA, l'argomento di questa nuova lezione sono i quadrilateri. Con l'aiuto della tartaruga Pitagora imparerete a disegnare quadrati, rombi, rettangoli e trapezi e a calcolare le loro principali informazioni geometriche.

Per iniziare dovete creare il pannello di controllo dove inserire le informazioni che servono alla tartaruga Pitagora per disegnare il tipo di quadrilatero scelto.
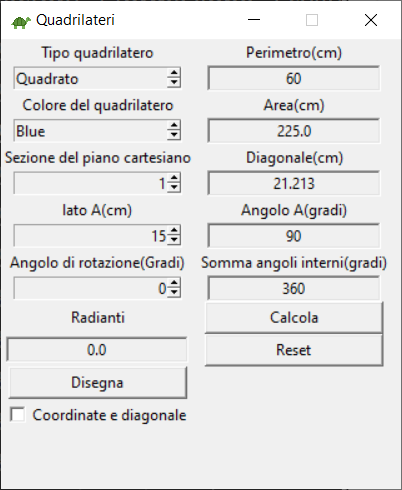
COME CREARE IL PANNELLO DI CONTROLLO PER DISEGNARE I QUATRILATERI
Per creare un'interfaccia grafica con Python dovete importare la libreria Tkinter con il comando seguente:
import tkinter as tk
Potete utilizzare l'alias tk per usare tutti i widget e le funzioni contenute all'interno di questa potente libreria grafica.
I widget più utilizzati sono: Label, Entry, Radiobutton, Checkbutton, Spinbox, Listbox, Button.
Per creare il pannello di controllo che servirà per disegnare i quadrilateri, utilizzeremo i seguenti widget: Label, Spinbox, Checkbutton, Button.
Potete creare la finestra che conterrà i widget con il comando seguente:
root = tk.Tk()
Ad esempio, il codice Python seguente vi permette di creare una finestra, larga 320 pixel ed alta 360 pixel, di disattivare il suo ridimensionamento ed impostare il titolo che apparirà in alto a sinistra:
root = tk.Tk()
root.geometry("320x360")
root.resizable(False,False)
root.title("Quadrilateri")
COME AGGIUNGERE I WIDGET ALLA FINESTRA TKINTER
Dopo la creazione della finestra tkinter, per aggiungere i widget che servono, li dovete prima creare e poi successivamente con le funzioni pack() oppure grid() li potete collegare.
La funzione pack() dispone i componenti in modo sequenziale, dall'alto verso il basso, permettendo di allinearli in alto, in basso, a sinistra e a destra, aggiungendo l'argomento side, come mostra l'esempio seguente:
root = Tk()
root.geometry('250x150')
button1 = Button(text="Left")
button1.pack(side = LEFT)
button2 = Button(text="Top")
button2.pack(side = TOP)
button3 = Button(text="Right")
button3.pack(side = RIGHT)
button4 = Button(text="Bottom")
button4.pack(side = BOTTOM)
root.mainloop()
La funzione grid() permette di disporre i componenti all'interno di una griglia, indicando la loro posizione attraverso la riga e la colonna.
L'esempio seguente mostra come potete aggiungere alla finestra root alcuni dei widget che vi servono:
root = tk.Tk()
root.geometry("320x360")
root.resizable(False,False)
root.title("Quadrilateri")
varTipo=tk.StringVar(root)
colore=tk.StringVar(root)
chkbt=tk.IntVar(root)
lbl_tipo=tk.Label(root,text="Tipo quadrilatero")
tipo=tk.Spinbox(root, values=["Quadrato", "Rombo", "Rettangolo", "Trapezio"], textvariable=varTipo, command=lambda: abilita_disabilita_controlli_pannello_quadrilateri(controlli_a,controlli_b), state="readonly")
lbl_colore=tk.Label(root,text="Colore del quadrilatero")
colore=tk.Spinbox(root,values=("None", "Blue", "Red", "Orange", "Green", "Yellow", "Violet", "Fuchsia", "Pink", "Deepskyblue", "Aqua", "Lightgreen", "Gold", "Peru", "Black", "Gray", "White"], textvariable=colore, state="readonly")
...
disegna = tk.Button(root, width=19, text ="Disegna", command = lambda:disegna_quadrilatero(varTipo.get(), int(rotazione.get()), int(lato_A.get()), int(lato_B.get()),colore.get(), int(sezione.get()), chkbt.get()))
coord_diag = tk.Checkbutton(root, text='Coordinate e diagonale',variable=chkbt,onvalue=1,offvalue=0)
...
lbl_tipo.grid(row=0,column=0)
tipo.grid(row=1,column=0)
lbl_colore.grid(row=2,column=0)
colore.grid(row=3,column=0)
disegna.grid(row=12,column=0)
coord_diag.grid(row=13,column=0)
...
root.mainloop()
Il comando root.mainloop() visualizza il pannello di controllo è si mette in ascolto degli eventi prodotti dagli utenti che usano l'interfaccia grafica.
Principalmente le azioni di un utente che sono associate ad un evento sono due: il click del mouse su un pulsante ed il cambiamento del contenuto di un widget, entrambi gli eventi possono essere associati all'esecuzione di una funzione con l'opzione command, come mostra il codice seguente:
disegna = tk.Button(root, width=19, text ="Disegna", command = lambda:disegna_quadrilatero(tipo.get(),int(rotazione.get()),int(lato_A.get()),int(lato_B.get()),colore.get(),int(sezione.get()),chkbt.get())),
quando l'utente clicca sul button disegna viene eseguita la funzione disegna_quadrilatero(...).
COME GESTIRE I VALORI ASSEGNATI AI WIDGET
Per gestire i valori contenuti nei widget di tipo input come ad esempio: Entry, Radiobutton, Checkbutton, Spinbox, Listbox, dovete associare il componente ad una variabile attraverso le opzioni textvariable o variable, come mostrano gli esempi seguenti:
Esempio 1
varTipo=tk.StringVar(root)
tipo=tk.Spinbox(root, values=["Quadrato", "Rombo", "Rettangolo", "Trapezio"], textvariable=varTipo, command=lambda: abilita_disabilita_controlli_pannello_quadrilateri(controlli_a,controlli_b), state="readonly")
Esempio 2
chkbt=tk.IntVar(root)
coord_diag = tk.Checkbutton(root, text='Coordinate e diagonale',variable=chkbt,onvalue=1,offvalue=0)
Le variabili varTipo e chkbt attraverso le opzioni textvariable e variable sono state associate ai widget tipo e coord_diag, in questo modo attraverso le due variabili potete leggere o assegnare un valore ai due componenti.
Per assegnare o leggere il valore di una variabile associata ad un widget dovete utilizzare le funzioni: set(valore) e get():
print(chkbt.get())
varTipo.set("Quadrato")
COME ELIMINARE UN WIDGET DA UNA FINESTRA TKINTER
Per eliminare un widget da una finestra Tkinter, dovete utilizzare la funzione pack_forget() se il componente è stato collegato con la funzione pack(), altrimenti dovete usare la funzione grid_forget(), come mostra l'esempio seguente:
tipo.grid_forget()
disegna.grid_forget()
Per eliminare velocemente tutti i widget di una finestra, potete aggiungere i loro indirizzi ad una lista ed utilizzare un ciclo for per eliminarli tutti con le funzioni grid_forget() oppure pack_forget(), come mostra la funzione seguente:
#Elimina controlli pannello quadrilateri
def elimina_controlli_pannello_quadrilateri(controlli_a,controlli_b):
for i in range(len(controlli_a)):
controlli_a[i].grid_forget()
for i in range(len(controlli_b)):
controlli_b[i].grid_forget()
Le liste controlli_a e controlli_b contengono i riferimenti a tutti i widget del pannello di controllo usato per gestire i quadrilateri:
lbl_tipo.grid(row=0,column=0)
controlli_a.append(lbl_tipo)
tipo.grid(row=1,column=0)
controlli_a.append(tipo)
lbl_colore.grid(row=2,column=0)
controlli_a.append(lbl_colore)
colore.grid(row=3,column=0)
controlli_a.append(colore)
lbl_sezione.grid(row=4,column=0)
controlli_a.append(lbl_sezione)
sezione.grid(row=5,column=0)
controlli_a.append(sezione)
lbl_lato_A.grid(row=6,column=0)
controlli_a.append(lbl_lato_A)
lato_A.grid(row=7,column=0)
controlli_a.append(lato_A)
LA GEOMETRIA DEL QUADRATO E DEL ROMBO
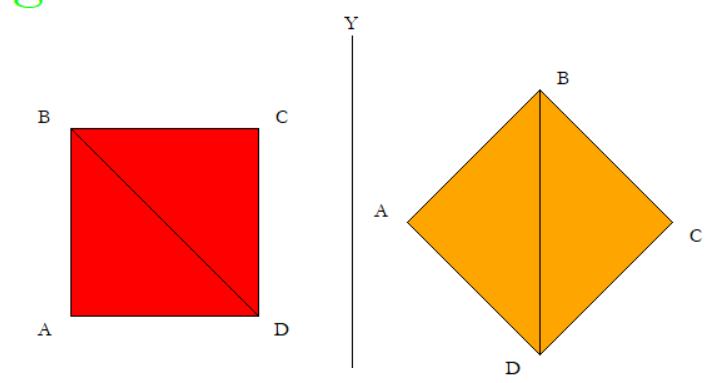
Il quadrato ed il rombo hanno le stesse caratteristiche geometriche, l'unica differenza è che il rombo ha un angolo di rotazione iniziale di 45 gradi.
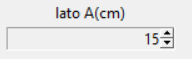
Per disegnare entrambe le figure basta un solo lato:
La diagonale di queste due figure geometriche si può calcolare applicando il teorema di pitagora.
Il codice Python seguente mostra come calcolare la diagonale, il perimetro e l'area, sia del quadrato, sia del rombo:
#Importare la libreria math
import math
#Diagonale
d=round(math.sqrt(math.pow(lato_A,2)+math.pow(lato_A,2)),3)
#Perimetro
p=lato_A*4
#Area
a=math.pow(lato_A,2)
Il codice Python seguente mostra come aggiornare i dati dei widget, nel pannello di controllo:
#Visualizzazione delle informazioni geometriche calcolate nel pannello di controllo
perimetro.config(text=str(p))
area.config(text=str(a))
diagonale.config(text=str(d))
L'angolo alfa adiacente al vertice A, come mostra l'immagine, misura 90°:
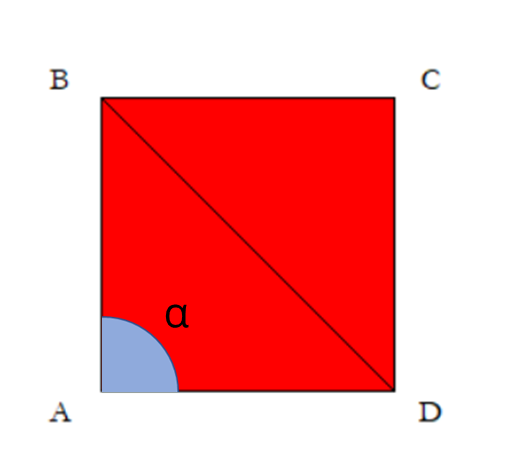
quindi la somma degli angoli interni del quadrato e del rombo corrisponde 360°.
#Angolo adiacente al vertice A
val_angolo_A=90
#Calcolo della somma degli angoli interni del quadrato e del rombo
val_angoli_somma=4*val_angolo_A
#Visualizzazione delle informazioni geometriche calcolate nel pannello di controllo
angolo_A.config(text=str(val_angolo_A))
angoli_somma.config(text=str(val_angoli_somma))
LA GEOMETRIA DEL RETTTANGOLO
Per disegnare un rettangolo occorrono due lati di lunghezza diversa, vi suggerisco di fare in modo che il lato_A sia quello minore ed il lato_B quello maggiore:

Anche in questo caso per calcolare la diagonale del rettangolo si può usare il teorema di pitagora.
Il codice Python seguente mostra come calcolare la diagonale, il perimetro e l'area, del rettangolo:
#Importare la libreria math
import math
#Diagonale
d=round(math.sqrt(math.pow(lato_A,2)+math.pow(lato_B,2)),3)
#Perimetro
p=(lato_A*2)+(lato_B*2)
#Area
a=lato_A*lato_B
#Visualizzazione delle informazioni geometriche calcolate nel pannello di controllo
perimetro.config(text=str(p))
area.config(text=str(a))
diagonale.config(text=str(d))
Anche nel rettangolo, l'angolo alfa adiacente al vertice A misura 90°:
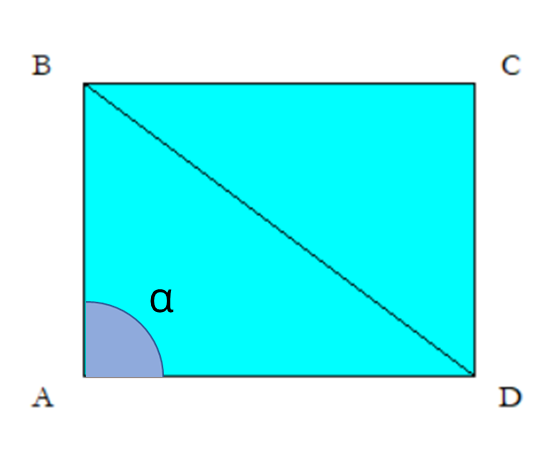
quindi la somma degli angoli interni del quadrato e del rombo corrisponde 360°.
#Angolo adiacente al vertice A
val_angolo_A=90
#Calcolo della somma degli angoli interni del rettangolo
val_angoli_somma=4*val_angolo_A
#Visualizzazione delle informazioni geometriche calcolate nel pannello di controllo
angolo_A.config(text=str(val_angolo_A))
angolo_B.config(text=str(val_angolo_B))
angoli_somma.config(text=str(val_angoli_somma))
LA GEOMETRIA DEL TRAPEZIO
Anche per disegnare un trapezio occorrono due lati di lunghezza diversa, vi suggerisco sempre di fare in modo che il lato_A sia quello minore ed il lato_B quello maggiore:

Il trapezio disegnato dalla tartaruga Pitagora è di tipo isoscele, con due lati obliqui uguali, come mostra l'immagine seguente:
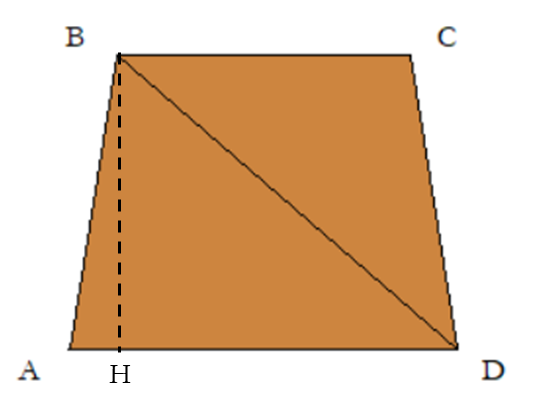
L'altezza BH corrisponde al lato_A, mentre la base HD del triangolo rettangolo bhd corrisponde al lato_A + AH, dove:
AH=(lato_B-lato_A)/2.
Per calcolare la diagonale del trapezio dovete applicare il teorema di pitagora ai cateti BH che corrisponde al lato_A e HD che corrisponde a lato_A+(lato_B-lato_A)/2, come mostra il codice Python seguente:
#Importare la libreria math
import math
#Diagonale
d=round(math.sqrt(math.pow(lato_A,2)+math.pow(lato_A+(lato_B-lato_A)/2,2)),3)
Per calcolare il perimetro del trapezio dovete prima calcolare la dimensione di uno dei lati obliqui, come mostra la formula seguente:
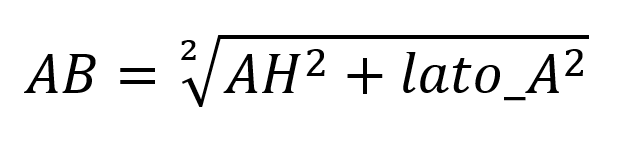
Il codice Python seguente vi permette di calcolare il perimetro del trapezio:
#Calcolo del lato obliquo
lo=round(math.sqrt(math.pow(lato_A,2)+math.pow((lato_B-lato_A)/2,2)),3)
#Perimetro
p=(lo*2)+lato_A+lato_B
Per calcolare l'area del trapezio dovete applicare la formula seguente:
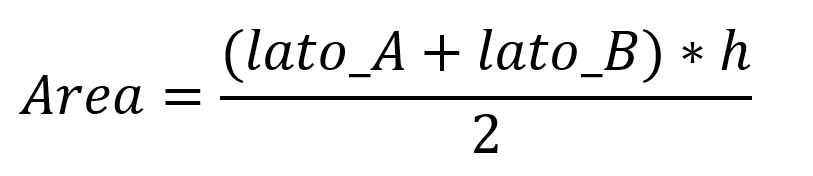
ll codice Python seguente mostra come calcolare l'area del trapezio:
#Area
a=((lato_A+lato_B)*lato_A)/2
Nel trapezio l'angolo alfa adiacente al vertice A è minore di 90° (acutangolo), perché i lati sono obliqui, ma la somma degli angoli interni continua ad essere uguale a 360°.
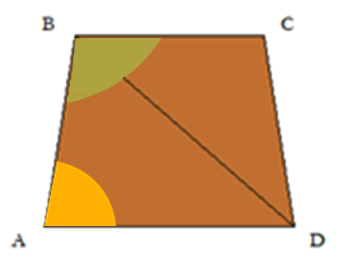
Per calcolare l'angolo alfa adiacente al vertice A dovete procedere come segue:
1) calcolare il seno dell'angolo alfa applicando la formula:
sin=lato_A/lato_Obliquo.
2) successivamente applicando la funzione inversa arcoseno si può ricavare la misura dell'angolo alfa in radianti.
3) per convertire i radianti in gradi applicare la funzione math.degrees(...).
Il codice Python seguente mostra come ottenere la misura espressa in gradi dell'angolo alfa, adiacente ad A:
#Angolo adiacente al vertice A
val_angolo_A=round(math.degrees(math.asin(lato_A/lo)),2)
L'angolo beta, adiacente al vertice B è maggiore di 90° (ottusangolo), per calcolarlo dovete fare due considerazioni:
1) il triangolo ABH è rettangolo, quindi l'angolo corrispondente al vertice H è di 90°.

2) la somma degli angoli interni di un triangolo è uguale a 180°.
Quindi l'angolo beta può essere calcolato come segue:
Angolo_ABH=(180-angolo_alfa-90)
Angolo beta=Angolo_ABH+90=180-angolo_alfa-90+90=180-angolo_alfa.
Il codice Python seguente mostra come ottenere la misura espressa in gradi dell'angolo alfa e dell'angolo beta, in modo da calcolare la somma degli angoli interni del trapezio:
val_angolo_A=round(math.degrees(math.asin(lato_A/lo)),2)
val_angolo_B=round(180-val_angolo_A,2)
val_angoli_somma=2*val_angolo_A+2*val_angolo_B
Usate il codice Python seguente per aggiornare le label della finestra dei quadrilateri:
perimetro.config(text=str(p))
area.config(text=str(a))
diagonale.config(text=str(d))
lato_obliquo.config(text=str(lo))
angolo_A.config(text=str(val_angolo_A))
angolo_B.config(text=str(val_angolo_B))
angoli_somma.config(text=str(val_angoli_somma))

COME DISEGNARE I QUADRILATERI
Per disegnare il quadrilatero scelto dovete prima posizionare la tartaruga Pitagora al centro della sezione del piano cartesiano scelta, la struttura condizionale seguente permette di impostare le coordinate richieste:
#Disegna il quadrilatero al centro del piano cartesiano
if sezione==0:
cx=0
cy=0
#Disegna il quadrilatero in alto a sinistra del piano cartesiano
elif sezione==1:
cx=-150
cy=150
#Disegna il quadrilatero in alto a destra del piano cartesiano
elif sezione==2:
cx=150
cy=150
#Disegna il quadrilatero in basso a sinistra del piano cartesiano
elif sezione==3:
cx=-150
cy=-150
#Disegna il quadrilatero in basso a destra del piano cartesiano
else:
cx=150
cy=-150
Il codice Python seguente permette di posizionare e ruotare la tartaruga Pitagora, prima che inizia a disegnare il quadrilatero:
turtle.goto(cx,cy)
turtle.setheading(270)
turtle.right(rotazione)
Il valore della variabile rotazione, se diverso da zero, permette di ruotare il quadrilatero del numero di gradi indicato, come mostra l'immagine seguente:

Nell'immagine lo stesso quadrato è stato disegnato più volte aggiungendo ogni volta una differenza di rotazione di 15°.
Nel codice Python allegato a questa lezione, nelle funzioni seguenti trovate il codice per disegnare i quadrilateri:
1) def disegna_quadrato_rombo(rotazione,lato_A,colore,sezione,coord_diag)
2) def disegna_rettangolo(rotazione,lato_A,lato_B,colore,sezione,coord_diag)
3) def disegna_trapezio(rotazione,lato_A,lato_B,colore,sezione,coord_diag).
COME DISEGNARE LE DIAGONALI E LE LETTERE DEI VERTICI
Per indicare alla tartaruga Pitagora di disegnare anche la diagonale e le lettere dei vertici dei quadrilateri, dovete selezionare il checbutton coordinate e diagonale.
Per memorizzare le posizioni necessarie per disegnare la diagonale e le lettere dei vertici dei quadrilateri, dovete creare un vettore di oggetti, del tipo seguente:
#Classe per memorizzare le coordinate delle figure geometriche
class MemorizzaCoordinate:
def __init__(self):
self.coordinate = []
def aggiungi(self,coordinata):
self.coordinate.append(coordinata)
def estrai(self):
posizione=self.coordinate[0]
del self.coordinate[0]
return posizione
def resetta(self):
self.coordinate.clear()
L'esempio seguente mostra come utilizzare la classe per memorizzare le posizioni necessarie e disegnare la diagonale e le lettere:
def disegna_rettangolo(rotazione,lato_A,lato_B,colore,sezione,coord_diag):
coordinateDiagonale=MemorizzaCoordinate()
coordinateLettere=MemorizzaCoordinate()
...
for x in range(2):
turtle.right(angoloRotazione)
coordinateLettere.aggiungi(turtle.pos())
turtle.forward(lato_A)
coordinateDiagonale.aggiungi(turtle.pos())
coordinateLettere.aggiungi(turtle.pos())
turtle.right(angoloRotazione)
turtle.forward(lato_B)
if colore!="None":
turtle.color(colore)
turtle.end_fill()
if coord_diag==1:
disegna_diagonale_lettere(cx,cy,coordinateDiagonale,coordinateLettere)
COME INSTALLARE ED ESEGUIRE L'APPLICAZIONE PITAGORA (VERSIONE 2)
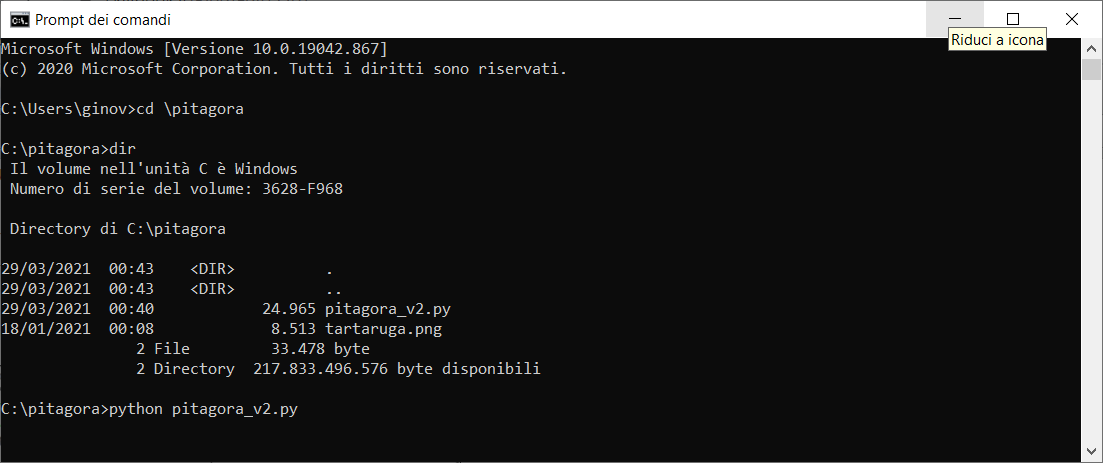
Per eseguire l'applicazione Pitagora sul vostro computer, la dovete prima scaricare cliccando qui.
Dopo il download del file pitagora_v2.zip che contiene i file: pitagora_v2.py e tartaruga.png, sul disco c: create la cartella pitagora, ed estraete all'interno i due file.
Per eseguire l'applicazione, da prompt scrivete il comando: python pitagora_v2.py, come mostra l'immagine seguente:
COME INSTALLARE PYTHON
Se non avete installato Python seguite i passaggi seguenti:
1) collegatevi al sito: https://www.python.org;
2) fate il download del file d'installazione;
3) Successivamente per installare Python, eseguite il file python-x.x.x.exe, dove x.x.x. è la versione che state installando;
4) Durante l'installazione non dimenticate di spuntare la selezione:

altrimenti Python si avvierà solo partendo dalla cartella dove verrà installato.
Per far parte della nostra community registrati su www.skillbook.it.
T U T O R I A L S S U G G E R I T I
- TypeScript
- Impariamo Python giocando al "Solitario del ferroviere"
- Impariamo a programmare con JavaScript
- Laboratori di Logica di programmazione in C
- Introduzione alla Logica degli oggetti
- Ricominciamo ... dal Linguaggio SQL
- APP Mania
- Come sviluppare un Sito con Wordpress
- Excel delle meraviglie
EDUCATIONAL GAMING BOOK (EGB) "H2O"
 Nell'era dello SMART LEARNING e di PYTHON i libri non si scrivono, ma si sviluppano, in questo modo chi studia, può sperimentare ed apprendere contemporaneamente; un libro con queste caratteristiche lo possiamo definire un Educational Gaming Book (EGB).
Nell'era dello SMART LEARNING e di PYTHON i libri non si scrivono, ma si sviluppano, in questo modo chi studia, può sperimentare ed apprendere contemporaneamente; un libro con queste caratteristiche lo possiamo definire un Educational Gaming Book (EGB).
"H2O" è un EGB che descrive tutte le caratteristiche dell'acqua, la sostanza formata da molecole di H2O, che attraverso il suo ciclo di vita garantisce la sopravvivenza di tutti gli esseri viventi del Pianeta.
L'obiettivo dell'EGB è quello di far conoscere ai giovani le proprietà dell'acqua, sotto molti aspetti uniche, per sensibilizzarli a salvaguardare un bene comune e raro, indispensabile per la vita.
Per il DOWNLOAD di "H2O" clicca qui.





 Le Tue Aule
Le Tue Aule
 I Tuoi Gruppi
I Tuoi Gruppi
 Le Tue Selezioni
Le Tue Selezioni



 Scheda Azienda
Scheda Azienda