Skill Factory
Tutte le categorie
1.Sei uno studente oppure un lavoratore? Scopri qual è il tuo livello di EQF.
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 06/03/2024 23:15:13 | in Home
Skill Factory - 06/03/2024 23:15:13 | in Home
 La formazione può essere formale, non formale e informale.
La formazione può essere formale, non formale e informale.
L'apprendimento formale segue regole e piani predefiniti, come avviene a scuola o attraverso i percorsi di formazione professionale, questo tipo di formazione è riconosciuto e può essere verificato e certificato.
L'apprendimento non formale è quello che avviene attraverso le esperienze formative personali o aziendali, fatte per approfondire le conoscenze e le abilità in uno specifico ambito di competenze e che servono per favorire la propria crescita professionale. Questo tipo di formazione è molto importante, ma può essere certificata da attestati oppure qualifiche non riconosciti dal sistema di formazione formale.
L'apprendimento informale avviene attraverso le esperienze risultanti dalle attività della vita quotidiana legate al lavoro, alla famiglia, al tempo libero. Questo tipo di formazione, pur essendo fondamentale per la vita di ogni cittadino, non può essere certificato, ma deve essere dimostrato attraverso la capacità di sapere e saper fare.
In Europa, prima del 2008, ogni nazione utilizzava un proprio sistema di formazione e qualifica. Con l'obiettivo di favorire la mobilità dei cittadini, le pari opportunità e un adeguato livello di formazione permanente, è stato istituito nel 2008 è aggiornato nel 2017 l'EQF.
L'EQF (European Qualifications Framework) è il Quadro Europeo delle Qualifiche, nasce allo scopo di comparare il livello d'istruzione e il livello di qualifica professionale degli studenti e dei lavoratori di tutta l'Europa.
Il Centro europeo per lo sviluppo della formazione professionale (Cedefop) e la Fondazione europea per la formazione (ETF), in quanto agenzie europee, svolgono un ruolo importante nel sostenere l'attuazione dell'EQF.
In Italia l'EQF è conosciuto come quadro nazionale delle qualificazioni (QNQ), rappresenta il dispositivo nazionale che favorisce le attività per rendere comparabili i livelli di studio e le qualifiche professionali degli studenti e dei lavoratori italiani, con quelli delle altre nazioni europee.
In linea con il quadro europeo delle qualifiche (EQF) , il QNQ si sviluppa su tre dimensioni:
1) conoscenze
2) abilita'
3) autonomia e responsabilita'.
Attraverso queste tre dimensioni si può descrivere il tipo di competenza che bisogna avere per raggiungere uno degli 8 livelli di qualificazione EQF, dove il livello 1 è il più basso e l'8 è il più alto.
Il QNQ è stato istituito nel 2013 dal MINISTERO DEL LAVORO E DELLE POLITICHE SOCIALI di concerto con il MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITA' E DELLA RICERCA.
Il Quadro nazionale delle qualificazioni è lo strumento che descrive e classifica le qualifiche rilasciate nell'ambito del Sistema nazionale di certificazione delle competenze.
Per leggere gli articoli del decreto pubblicati sulla "Gazzetta Ufficiale", clicca qui.
Per avere una mappa dettagliata del lavoro e delle qualificazioni, del nostro Sistema nazionale di certificazione delle competenze, puoi consultare l'ATLANTE DEL LAVORO E DELLE QUALIFICAZIONI.
L'Atlante nasce dal lavoro di ricerca condotto dall'INAPP (Istituto Nazionale Per l'Analisi delle Politiche Pubbliche), con la partecipazione di diversi soggetti istituzionali, delle parti datoriali e sindacali, delle rappresentanze bilaterali, delle associazioni professionali, degli esperti settoriali e degli stakeholder del sistema lavoro-learning.
Per accedere all'ATLANTE DEL LAVORO E DELLE QUALIFICAZIONI, clicca qui.
La tabella seguente mostra la corrispondenze tra i livelli EQF e i titoli di studio che si possono coseguire in Italia:
Livello EQF | Tipologia di qualificazione
1 Diploma di licenza conclusiva del I ciclo di istruzione
2 Certificazione delle competenze di base acquisite in esito all'assolvimento dell'obbligo di istruzione
3 Attestato di qualifica di operatore professionale
4 Diploma professionale di tecnico, Diploma liceale, Diploma di istruzione tecnica, Diploma di istruzione professionale, Certificato di specializzazione tecnica superiore
5 Diploma di tecnico superiore
6 Laurea, Diploma Accademico di I livello
7 Laurea Magistrale, Diploma Accademico di II livello, Master universitario di I livello, Diploma Accademico di specializzazione (I), Diploma di perfezionamento o master (I)
8 Dottorato di ricerca, Diploma accademico di formazione alla ricerca, Diploma di specializzazione, Master universitario di II livello, Diploma Accademico di specializzazione (II), Diploma di perfezionamento o master (II)
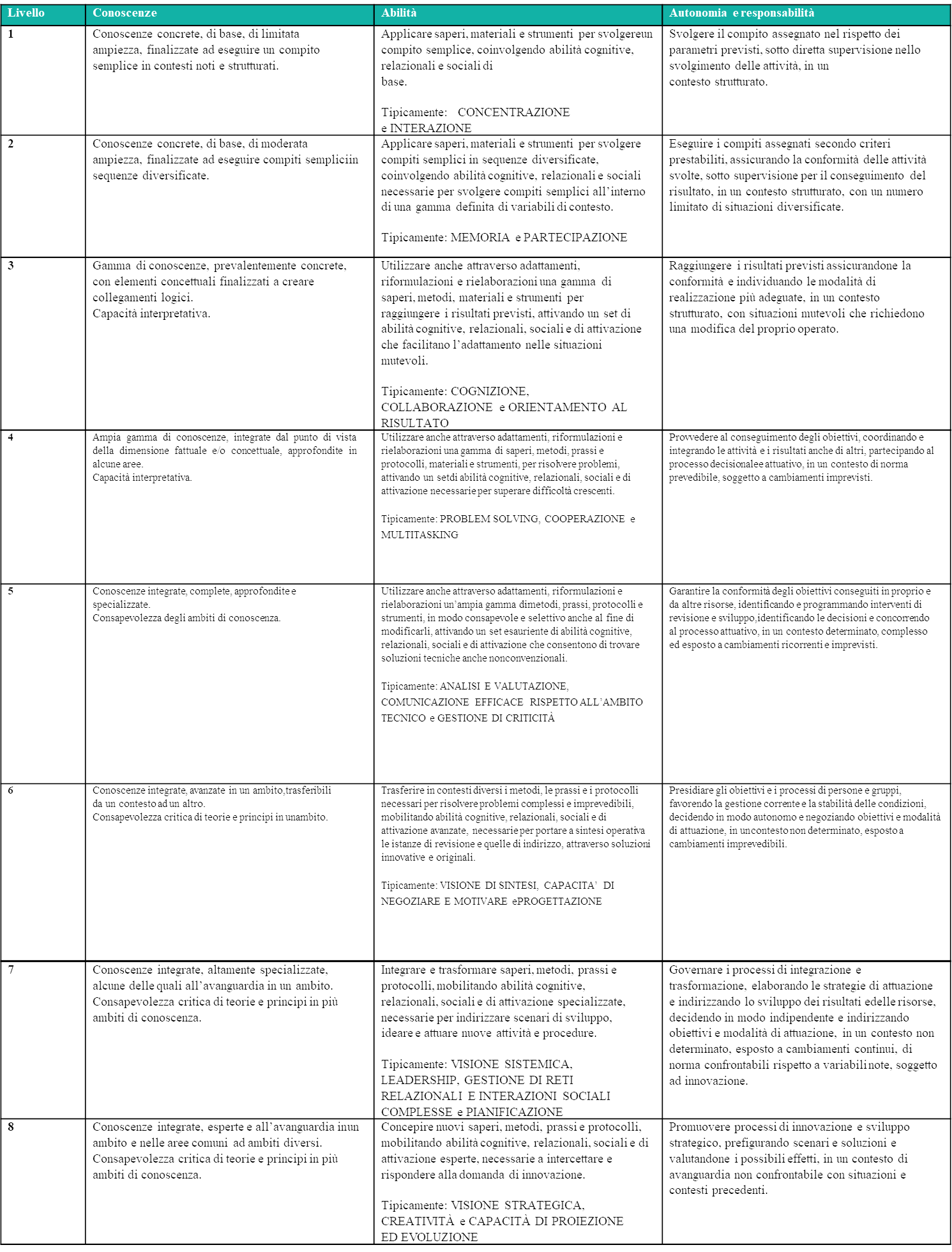
Utilizzando la tabella seguente, puoi individuare il livello EQF che corrisponde al tuo profilo professionale in base al livello di conoscenza, abilità, autonomia e responsabilità raggiunto:
Approfondimenti:
6.L'Assicurazione della Qualità nell'IFP.
5.L'Etica della formazione come responsabilità professionale.
4 Buona Formazione: "Come assicurare la qualità della formazione".
3.La qualità della formazione inizia dal confronto.
2.La filiera della Formazione Professionale in Europa e in Italia.

Per informazioni e contatti: www.skillfactory.it
Il 2024 è un anno bisestile. In programmazione come facciamo a capire se un anno è secolare e bisestile?
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 02/03/2024 12:20:59 | in Home
Skill Factory - 02/03/2024 12:20:59 | in Home
Il 2024 è un anno bisestile, perché febbraio è di 29 giorni. Questo significa che il 2024 durerà 366 giorni e non 365 giorni come accade per gli anni non bisestili.
Nel calendario Gregoriano è bisestile un anno ogni 4, questa correzione è necessaria perché astronomicamente un anno solare dura circa 365,25 giorni.
Se non tenessimo conto di questa variazione, ogni 4 anni si accumulerebbe un ritardo di un giorno. I continui ritardi accumulati nel tempo, modificherebbero le date delle stagioni che corrispondono agli equinozi di primavera e autunno e i solstizi d'estate e inverno, spostandole in avanti nel tempo.
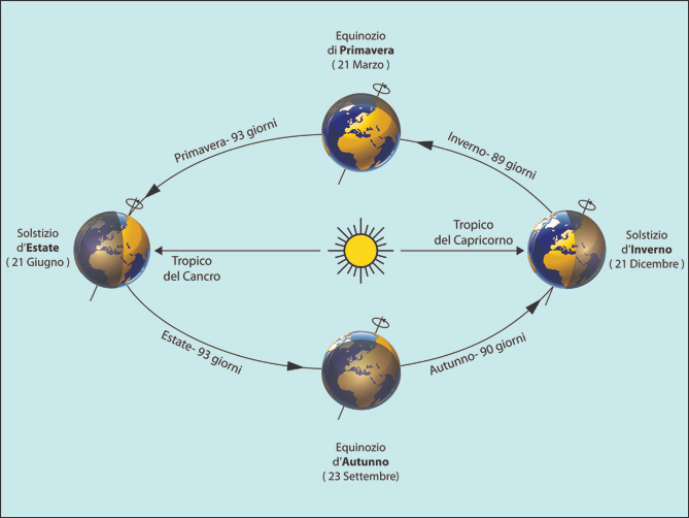
Gli anni secolari, ovvero quelli divisibili per 100, sono bisestili se oltre ad essere divisibili per 100 sono divisibili anche per 400. Quindi un anno è sicuramente bisestile se è divisibile per 400.
Ad esempio il 1600 è bisestile perché è divisibile per 400, mentre il 1700 non è bisestile perché non è divisibile per 400.
Gli anni non secolari sono bisestili solo se sono divisibili per 4.
Quindi, un programmatore, per verificare se un anno è bisestile, deve prima controllare se è secolare, in caso affermativo deve anche vedere se è divisibile per 400. Se l'anno non è secolare, per essere bisestile deve essere divisibile per 4.
Il programma Python seguente, ci permette di verificare se un anno è secolare e bisestile:
# Verifica se l'anno è bisestile
# Funzione
def tipo_anno():
try:
messaggio="L'anno "+str(v_anno.get())+" "
if v_anno.get()%100==0:
messaggio=messaggio+"è secolare e "
if v_anno.get()%400==0:
messaggio=messaggio+"bisestile."
else:
messaggio=messaggio+"non è bisestile."
else:
messaggio=messaggio+"non è secolare e "
if v_anno.get()%4==0:
messaggio=messaggio+"bisestile."
else:
messaggio=messaggio+"non è bisestile."
tk.messagebox.showinfo(title='Informazioni', message=messaggio)
except:
messaggio="Inserisci l'anno da verificare"
tk.messagebox.showinfo(title='Errore', message=messaggio)
def reset():
v_anno.set("")
# Programma
import tkinter as tk
from tkinter.messagebox import showinfo
root=tk.Tk()
root.geometry('350x100+150+150')
root.resizable(False, False)
root.title('Verifica anno secolare e bisestile')
v_anno=tk.IntVar(root,"")
lbl_anno=tk.Label(root,text="Inserisci l'anno per verificare se è secolare e bisestile").pack(pady=5)
txt_anno=tk.Entry(root, justify="right",textvariable=v_anno).pack(pady=5)
frm_button=tk.Frame(root)
btn_verifica=tk.Button(frm_button,text="VERIFICA",command=tipo_anno).pack(side=tk.LEFT)
btn_reset=tk.Button(frm_button,text="RESET",command=reset).pack(side=tk.RIGHT)
frm_button.pack()
root.mainloop()
Se sei interessato ad approfondire questo argomento, clicca qui, per imparare a creare un calendario perpetuo con Python.
Al via i corsi di specializzazione dell'Academy delle professioni digitali - "Skill Factory".
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 23/02/2024 15:16:10 | in Formazione e lavoro
Skill Factory - 23/02/2024 15:16:10 | in Formazione e lavoro
Da marzo sono aperte le iscrizioni per partecipare ai corsi di specializzazione dell'Academy delle professioni digitali. Un progetto innovativo - firmato Skill Factory - per creare gli specialisti del digitale che servono alle aziende che vogliono essere competitive.
L'Academy, diretta da Gino Visciano, con il suo team di esperti in formazione digitale, ti permette di acquisire le competenze trasversali, tecniche e manageriali, per creare uno dei 6 profili professionali più richiesti dal mercato del lavoro digitale:
Clicca sull'immagine per accedere al dettaglio dei corsi.
È garantita:
- Alta professionalità tecnica e didattica
- Lezioni online con docente
- Laboratori asincroni reali, con supporto remoto in smart working
- Flessibilità per permettere anche a chi studia o lavora di seguire i corsi
- Pagamento mensile
- Assistenza alla compilazione del cv
- Presentazione del cv ai Job Partner della Skill Factory
- Orientamento e preparazione al colloquio di lavoro
- Digital badge che attesta la partecipazione al corso e certifica le competenze acquisite.
Per finalizzare l’iscrizione al corso sarà necessario versare la prima rata mensile con possibilità di recesso entro il primo mese.
Per informazioni e contatti:
sito: www.skillfactory.it
cell.: 3270870141
tel.: 08118181361
2. Competenze per programmare: Mondo Reale e Mondo Digitale
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 25/02/2023 10:16:25 | in Tutorials
Skill Factory - 25/02/2023 10:16:25 | in Tutorials

Nell'era della trasformazione digitale è importante capire la differenza tra "Mondo reale" e "Mondo digitale".
Oggi, mondo reale e mondo digitale, coesistono, ampliando lo spazio fisico in cui viviamo con quello cibernetico, che può essere considerato come un Universo parallelo, alternativo a quello fisico.
Il mondo reale è quello in cui viviamo, composto dalle cose che osserviamo e tocchiamo, quello digitale è il mondo delle cose che assumono la forma di numeri binari.
Il mondo digitale esiste grazie al Ciberspazio (Cyberspace), la rete delle reti, chiamta Internet, che interconnette tutti i sistemi informatici ed elettronici del mondo, su cui girano i software e le applicazioni che permettono il funzionamento di Internet e del mondo cibernetico.

Il termine è stato utilizzato la prima volta nel 1982, nella forma inglese cyberspace, in un racconto di fantascienza dal titolo "Burning Chrome".
I tipi di applicazioni più conosciuti del cyberspace sono i seguenti:
- Social media;
- Social network;
- Motori di ricerca;
- Portali;
- Siti Web;
- Blog;
- E-Commerce;
- E-Learning
- Community;
- Suite applicative;
- Etc..
Qual è la diiferenza tra mondo reale e mondo digitale?
La risposta è semplice, il mondo reale è fatto di informazioni analogiche, quello digitale è fatto di cifre binarie, perché gli apparecchi elettronici possono gestire solo due stati fisici (flip-flop), che noi identifichiamo con le cifre 0 e 1, chiamate bit (Binary Digit).

Come sono fatte le informazioni analogiche?
Tutto cio che percepiamo nel mondo reale ha una forma analogica. Senza scendere in tenicismi complessi, possiamo dire che tutto quello che vedete o ascoltate, sotto forma di immagini o suoni, fatto di punti, linee oppure onde, è analogico.
Gli apparecchi elettronici, a differenza degli uomini, non possono memorizzare le immagini e i suoni in forma analogica, ma lo possono fare in forma digitale; sequenze di cifre binarie chiamate bit.
Fisicamente i bit negli apparecchi elettronici corrispondono a sequenze di interruttori (Flip-Flop) che possono assumere lo stato 0 oppure 1.
La cosa importante è che qualunque informazione analogica può essere trasformata in digitale e viceversa.
E' vero che le informazioni digitali sono più precise di quelle analogiche?
Si, è vero. I numeri sono grandezze precise, le immagini e i suoni possono anche essere interpretati male; questo è evidente con gli orologi.
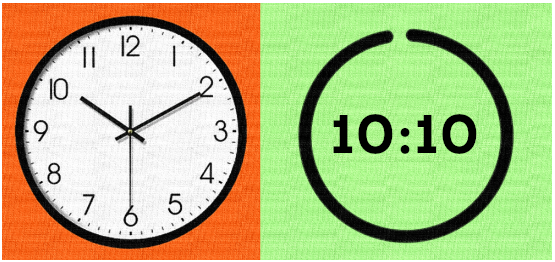
Un orologio anlagico indica le ore, i minuti e i secondi attraverso tre lancette diverse, la posizione delle lancette, quando viene letta l'ora, può essere interpretata male e la persona potrebbe leggere un informazione non esatta.
Un orologio digitale indica le ore, i minuti e i secondi attraverso cifre, in questo caso l'ora letta è sempre esatta.
In che modo le informazioni analogiche possono essere trasformate in digitali?
La risposta a questa domanda complessa, può diventare semplice se facciamo riferimento all'informatica.
Quando scrivete qualcosa con un dispositivo elettronico, utilizzate la tastiera:

Tutti i caratteri della tastiera, noi li percepiamo come informazioni analogiche, perchè sono composti da punti e linee, quindi il testo che scriviamo noi lo possiamo ricordare, il dispositivo che stiamo usando no.
Per permettere al dispositivo elettronico di memorizzare i caratteri usati per scrivre un testo, devono essere convertiti in numeri; per questo motivo è nata la tabella dei codici ASCII (pronuncia ASKII) che associa a 256 caratteri diversi, un numero da 0 a 255:
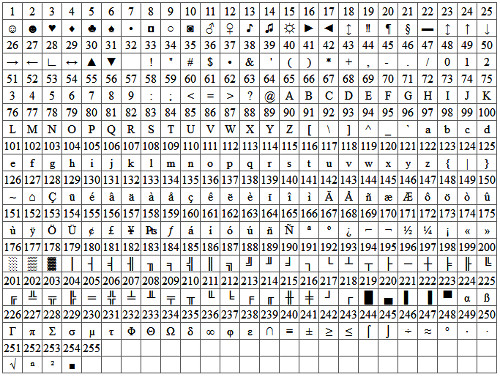
Per approfondire la conoscenza del codice ASCII clicca qui.
Ad esempio, se digitate un carattere "A" oppure un carattere "1", entrabi vengono prima convertiti nei rispettivi codici ASCII 65 e 49, successivamente i numeri decimali vengono convertiti in banario, per permettere al dispositivo elettronico di memorizzarli attraverso sequenze di 8 flip-flop (interruttori elettrici), capaci di rappresentare i bit 0 oppure 1:
A=6510=010000012
1=4910=001100012
L'immagine seguente mostra le fasi di conversione di un messaggio ti tipo testo in binario:
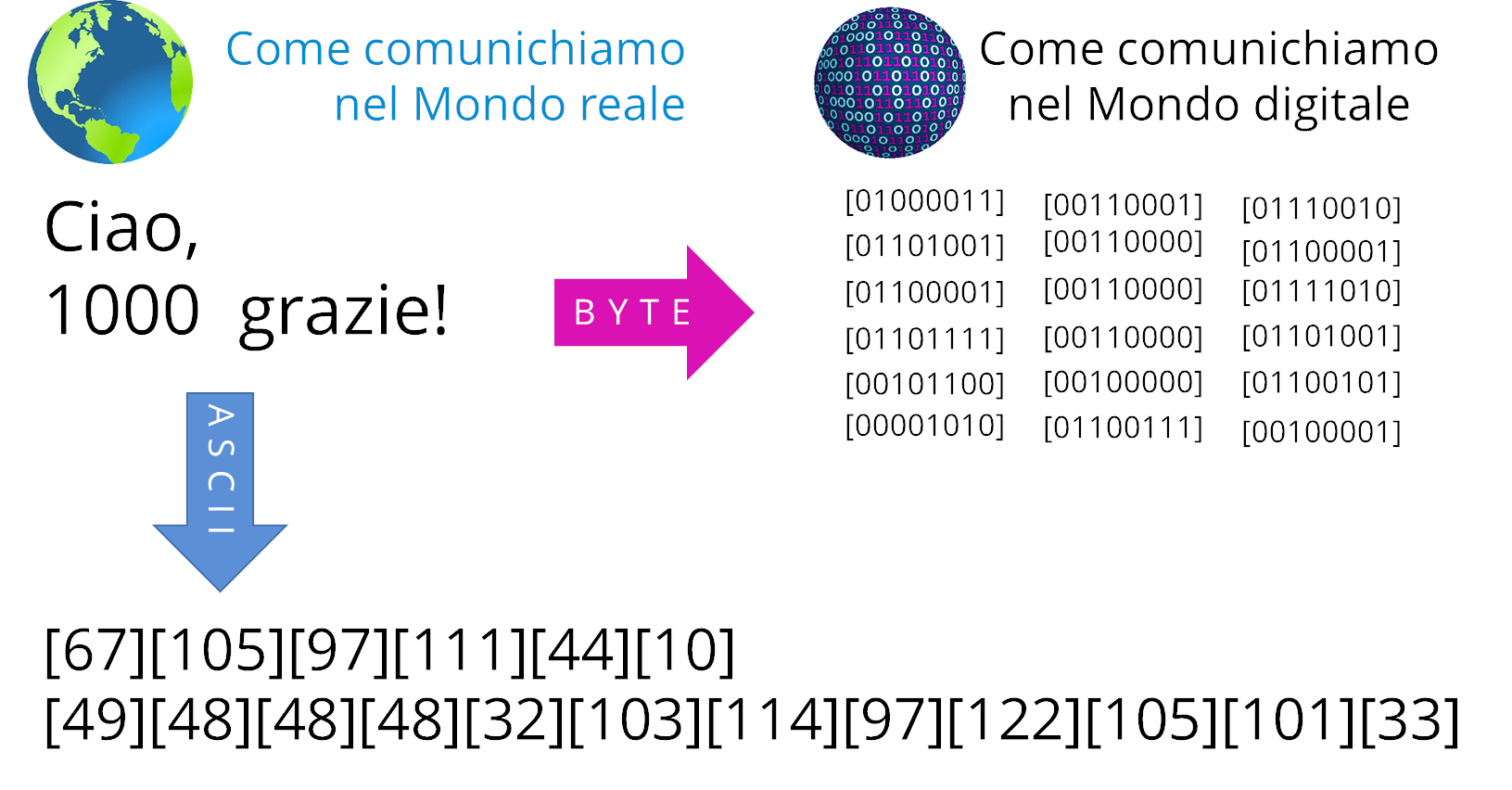
Ricordate che per indicare in binario il numero 255, che corrisponde all'ultimo carattere del codice ASCII, servono otto cifre (bit); per questo motivo l'unità di misura minima dell'informatica è il byte (8 bit).
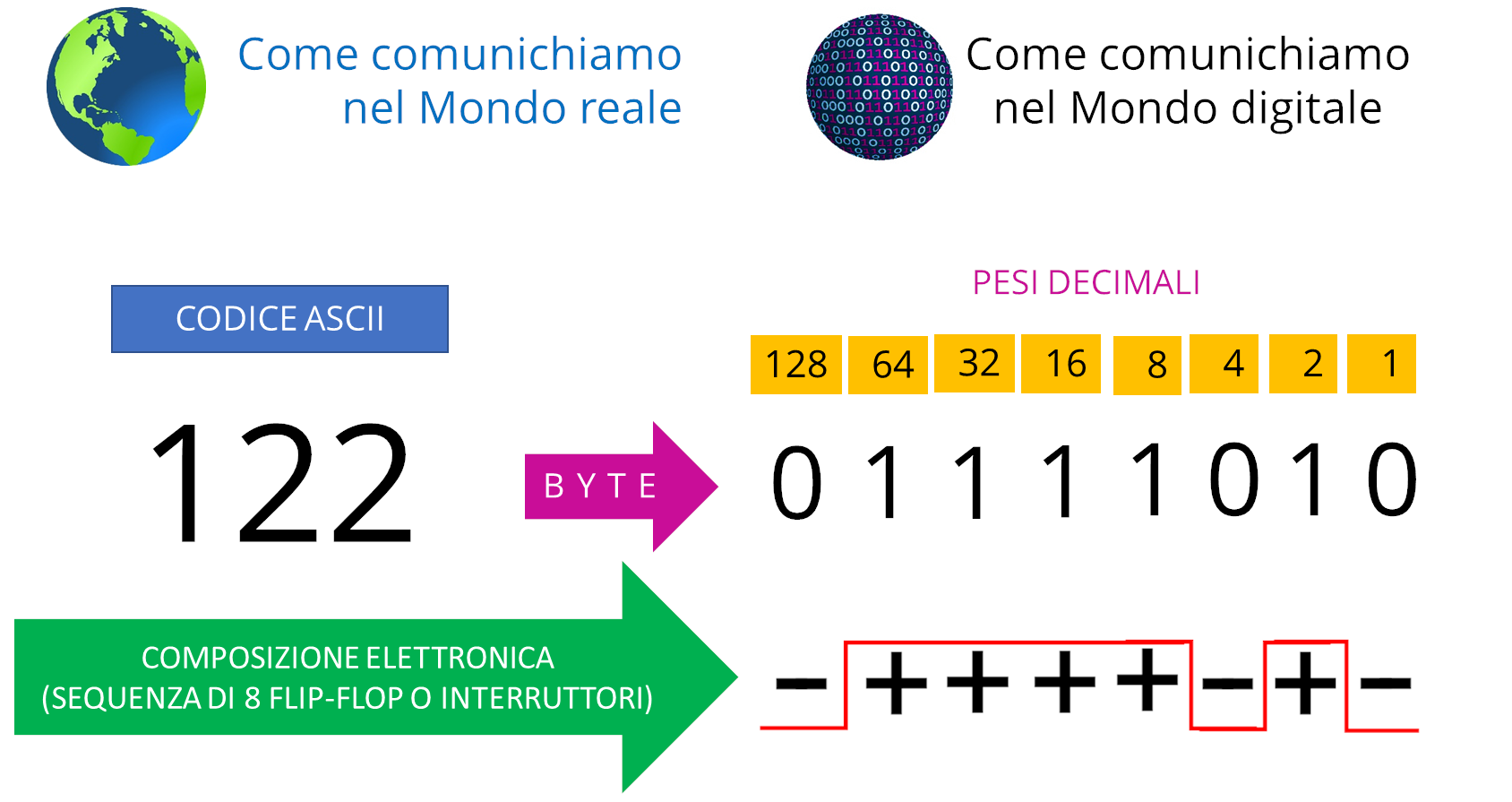
Anche le immagini composte da punti o linee e i suoni formati da onde sinusoidali, possono essere convertiti in sequenze di byte, in questo modo possono essere memorizzati dai dispositivi elettronici.
L'immagine seguente mostra forme diverse di onde sonore in forma analogica:

PRINCIPALI STRUMENTI DEL MONDO REALE E DEL MONDO DIGITALE
- COLORI

- IMMAGINI

- SUONI

- POSTA

- LIBRI

- CHIAVI

- FIRME

- SOLDI

- MAGAZZINO

IDENTITA' DIGITALE
- INTELLIGENZA ARTIFICIALE

- REALTA AUMENTATA O METAVERSO

Quali rischi corriamo quando siamo connessi al mondo digitale?
Come per il modo reale, anche in quello digitale si corrono dei rischi, quindi bisogna stare molto attenti a non assumere comportamenti sbagliati.
Quando siete connessi ad Internet con la vostra identità digitale e comunicate con qualcuno, state attenti, perché non sempre chi sta dall'altra parte è realmente chi dice di essere!!!
Non fidatevi di chi vi propone cose strane, ma soprattutto prima di fare qualunque cosa che vi viene richiesta, confidatevi con qualcuno molto vicino a voi.
Un altro rischio molto diffuso quando siete interconnessi ad Internet, è quello del furto d'informazioni riservate come ad esempio:
- Carta d'identità;
- Informazioni di genere, politiche, religiose;
- Password di carte di credito, bmt, conti correnti, etc..
Questa attività, chiamata "Phishing", spesso avviene attraverso l'installazione sul proprio computer di software malevoli, chiamati malware.
Per evitare questo tipo di attacchi, bisogna installare sul proprio computer un buon antivirus, non aprire allegati di mail sospette e non navigare su siti non conosciuti.

Infine attenti ai bulli, perché potreste trovarli anche nel mondo digitale.
Purtroppo in Internet, il fenomeno del cyberbullismo è molto comune; sia nella vita reale, sia in quella digitale. Anche se avete paura non dovete mai subire minacce da parte di altre persone, le conseguenze potrebbero essere molto gravi.
Se siete vitteme o conoscete qualcuno che è vittima di bullismo o cyberbullismo, è sempre meglio denunciare subito l'accaduto a qualcuno molto vicino a voi o alla polizia!!!

INFORMATICA APPLICATA
Laboratorio
Creare un programma che trasforma un messaggio di tipo testo in ASCII e in binario (Byte).
Soluzione JavaScript
// Funzioni
function decimaleBinario(decimale) {
var binario = [];
var numero = 0;
var posizione = 7;
for (var x = 0; x < 8; x++) {
binario.push(0);
}
numero = decimale;
while (numero >= 2) {
risultato = Math.floor(numero / 2);
resto = numero % 2;
binario[posizione] = resto;
posizione--;
numero = risultato;
}
binario[posizione] = numero;
return binario.join('');
}
// Programma
var input = require("readline-sync");
var messaggio = "";
var risposta = "";
var riga = "";
var ascii = [];
var binario = [];
var x = 0;
do {
ascii = [];
binario = [];
messaggio = input.question("Messaggio da convertire: ");
for (var x = 0; x < messaggio.length; x++) {
ascii.push(messaggio.charCodeAt(x));
binario.push(decimaleBinario(messaggio.charCodeAt(x)));
}
console.log("Conversione del messaggio in ASCII:");
riga = "";
for (x = 0; x < ascii.length - 1; x++) {
riga = riga + ascii[x] + ","
}
riga = riga + ascii[x] + "."
console.log(riga);
console.log("Conversione del messaggio in binario (Byte):");
riga = "";
for (x = 0; x < binario.length - 1; x++) {
riga = riga + binario[x] + ","
}
riga = riga + binario[x] + "."
console.log(riga);
risposta = input.question("Vuoi inserire un altro messaggio (s/n)? ")
while (risposta.toLowerCase() != 's' && risposta.toLowerCase() != 'n') {
console.log("Errore: inserire s oppure n.");
risposta = input.question("Vuoi inserire un altro messaggio (s/n)? ")
}
} while (risposta.toLowerCase() == 's');
Soluzione Python
import math
# Funzioni
def decimaleBinario(decimale):
binario = []
numero = 0
posizione = 7
for x in range(8):
binario.append('0')
numero = decimale
while numero >= 2:
risultato = math.floor(numero / 2)
resto = numero % 2
binario[posizione] = str(resto)
posizione = posizione-1
numero = risultato
binario[posizione] = str(numero)
return ''.join(binario)
# Programma
messaggio = ''
risposta = 's'
riga = ''
ascii = []
binario = []
x = 0
while risposta == 's':
ascii = []
binario = []
messaggio = input("Messaggio da convertire: ")
for carattere in messaggio:
ascii.append(ord(carattere))
binario.append(decimaleBinario(ord(carattere)))
print("Conversione del messaggio in ASCII:")
riga = ""
for x in range(len(ascii)-1):
riga = riga + str(ascii[x]) + ","
x=x+1
riga = riga + str(ascii[x]) + "."
print(riga)
print("Conversione del messaggio in binario (Byte):")
riga = ""
for x in range(len(binario)-1):
riga = riga + binario[x] + ","
x=x+1
riga = riga + binario[x] + "."
print(riga)
risposta = input("Vuoi inserire un altro messaggio (s/n)? ")
while risposta != 's' and risposta != 'n':
print("Errore: inserire s oppure n.")
risposta = input("Vuoi inserire un altro messaggio (s/n)? ")
Come eseguire il programma JavaScript
Per eseguire il programma JavaScript, bisogna installare il framework node.js sul proprio computer.
Il download del file d'installazione può essere fatto collegandosi al link: https://nodejs.org/it/download/.
Il file di download deve corrispondere al sistema operativo installato sul proprio computer.
Dopo il download eseguire il file per installare node.js.
Per verificare se il framework node.js è stato installato correttamente, dal prompt dei comandi del sistema operativo usato, eseguire il comando:
node --version
dovrebbe essere visualizzata la versione di node.js installata, come mostra l'immagine seguente:
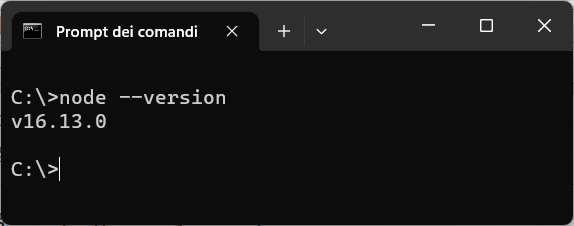
Successivamente bisogna creare una cartella "laboratori" dove salvare il programma JavaScript da eseguire.
Per salvare il programma nella cartella "laboratori", basta copiarlo nel blocco note o in qualunque editor di testo e salvarlo con il nome:
analogico_digitale.js
Infine, da prompt dei comandi, entrare nella cartella laboratori ed eseguire il comando:
npm install readline-sync
Questa libreria serve per permettere l'inserimento di dati da tastiera, quando viene eseguito il programma.
A queso punto si può eseguire il programma con il comando node, che è l'interprete JavaScript di node.js, come mostra l'esempo seguente:
node analogico_digitale
Come eseguire il programma Python
Per eseguire il programma Python, bisogna installare il framework python sul proprio computer.
Il download del file d'installazione può essere fatto collegandosi al link: https://www.python.org/downloads/.
Il file di download deve corrispondere al sistema operativo installato sul proprio computer.
Dopo il download eseguire il file per installare python.
Attenzione, durante l'installazione è importante spuntare l'opzione "Add Python 3.X to PATH:
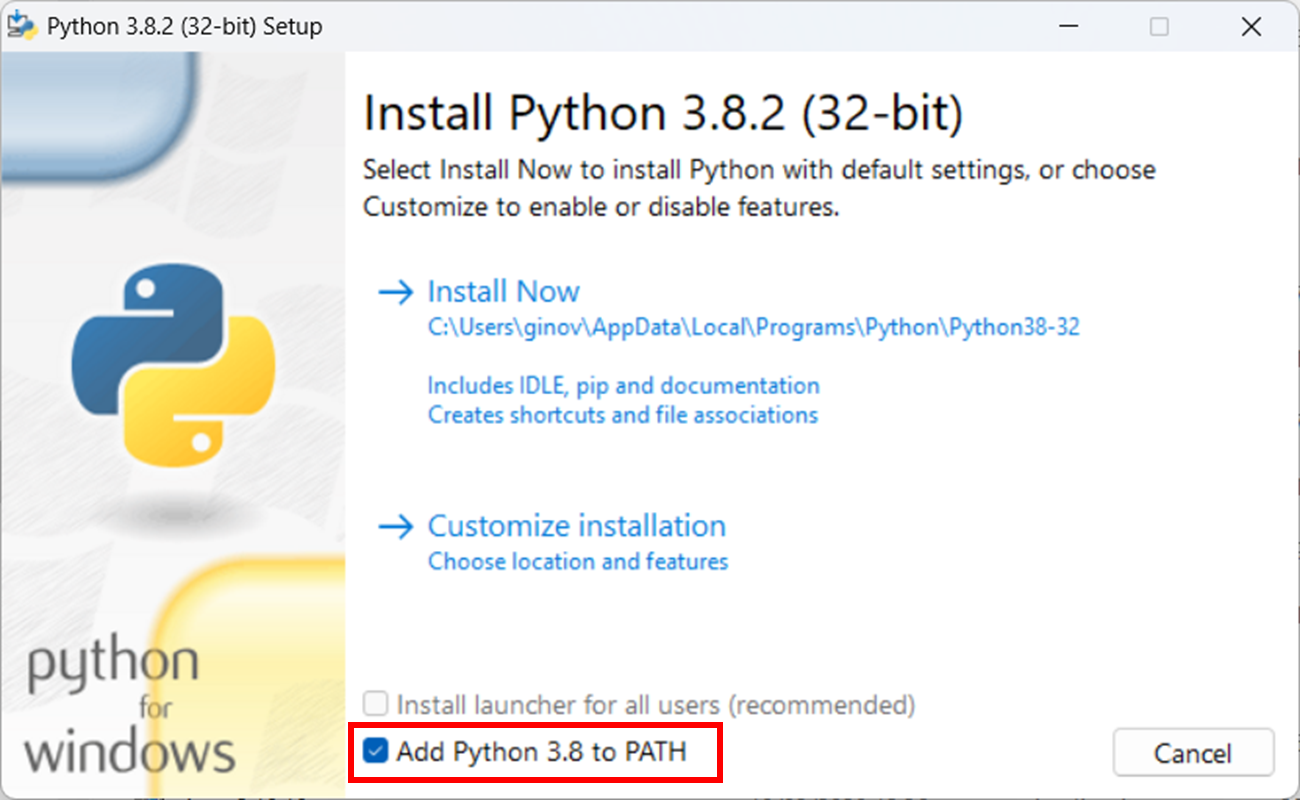
Per verificare se il framework python è stato installato correttamente, dal prompt dei comandi del sistema operativo usato, eseguire il comando:
python --version
dovrebbe essere visualizzata la versione di python installata, come mostra l'immagine seguente:
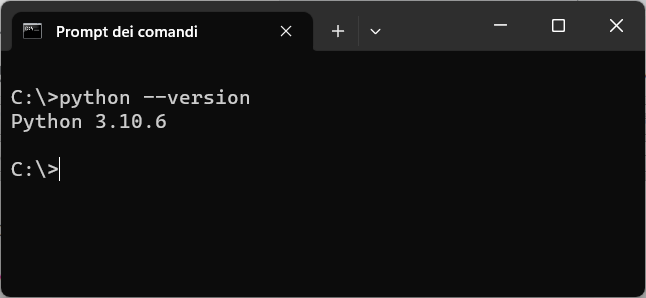
Successivamente bisogna creare una cartella "laboratori" dove salvare il programma python da eseguire.
Per salvare il programma nella cartella "laboratori", basta copiarlo nel blocco note o in qualunque editor di testo e salvarlo con il nome:
analogico_digitale.py
Infine, da prompt dei comandi, entrare nella cartella laboratori ed eseguire il comando:
python analogico_digitale.py
Leggi anche le altre lezioni ...
COMPETENZE PER PROGRAMMARE:
1-I sistemi di numerazione
3-La reppresentazione digitale dei numeri interi e decimali
4-Le stringhe
5-Le espressioni regolari (REGEXP)
6-Date, ore e fusi orari
Segui sul canale YouTube "Skill Factory Channel" la Playlist: COMPETENZE PER PROGRAMMARE
TUTORIALS
1-Laboratori di logica di programmazione in C
2-Impariamo a programmare con JavaScript
3-Ricominciamo dal linguaggio SQL
4-Introduzione alla logica degli oggetti
5-TypeScript
6-Impariamo a programmare in Python
7-Come sviluppare un sito in WordPress
PAR GOL (Garanzia di Occupabilità dei Lavoratori)

Se sei residente in Campania e cerchi lavoro, sai che puoi partecipare gratuitamente ad un corso di formazione professionale PAR GOL?
I corsi di formazione professionale PAR GOL sono finanziati dalla Regione Campania e ti permettono di acquisire una Qualifica Professionale Europea (EQF) e di partecipare ad un tirocinio formativo aziendale.
Invia il tuo CV o una manifestazione d'interesse a: recruiting@skillfactory.it
oppure
chiama ai seguenti numeri di telefono:
Tel.: 081/18181361
Cell.: 327 0870141
oppure
Contattaci attraverso il nostro sito: www.skillfactory.it
Per maggiori informazioni sul progetto PAR GOL, clicca qui.
Per maggiori informazioni sulle Qualifiche Professionali Europee (EQF), clicca qui.
Academy delle professioni digitali
Per consultare il catalogo dei corsi online della nostra Academy ...

... collegati al nostro sito: www.skillfactory.it
1. Competenze per programmare: i sistemi di numerazione
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 19/02/2023 17:01:17 | in Tutorials
Skill Factory - 19/02/2023 17:01:17 | in Tutorials

Introduzione ai sistemi di numerazione
I sistemi di numerazione più usati nell'ambito informatico sono:
1) il sistema decimale a base 10 perché per comporre i numeri utilizza le cifre (0,1,2,3,4,5,6,7,8,9)
2) il sistema binario a base 2 perché per comporre i numeri utilizza le cifre (0,1) chiamate bit (binary digit)
3) il sistema ottale a base 8 perché per comporre i numeri utilizza le cifre (0,1,2,3,4,5,6,7)
4) il sistema esadecimale a base 16 perché per comporre i numeri utilizza le cifre (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F)
Il sistema decimale (dec) è quello usato dagli uomini, che contando con le dieci dita delle mani trovano più conveniente usare dieci cifre.

Il sistema binario (bin) è quello usato dai computer, che per contare hanno solo due stati, acceso=1 o spento=0, che corrispondono a interruttori elettronici chiamati flip-flop.

Sequenze di flip-flop (interruttori elettronici a due stati spento=0 e acceso=1) permettono di scrivere i numeri in forma binaria, ovvero come sequenze di bit (0/1).
I numeri binari sono difficili da ricordare perché sono composti da troppe cifre, per questo motivo spesso vengono convertiti in ottale (ott o oct) oppure in esadecimale (esa o hex).
Ad esempio, numeri binari composti da tre bit possono essere rappresentati con una sola cifra ottale:
[Bin] [Ott]
000 = 0
001 = 1
010 = 2
011 = 3
100 = 4
101 = 5
110 = 6
111 = 7
Se i numeri binari sono composti da quattro bit, allora conviene rappresentarli con una cifra esadecimale, come mostra l'esempio seguente:
[Bin] [Esa]
0000 = 0
0001 = 1
0010 = 2
0011 = 3
0100 = 4
0101 = 5
0110 = 6
0111 = 7
1000 = 8
1001 = 9
1010 = A
1011 = B
1100 = C
1101 = D
1110 = E
1111 = F
In informatica l'unità minima di misura è il byte che corrisponde ad otto bit. Questo significa che qualunque apparecchio elettronico quando legge o scrive i numeri binari lo fa con otto bit contemporaneamente.
Per rappresentare il valore di un byte composto da otto cifre binarie (bit), bastano semplicemente due cifre esadecimali.
Ad esempio:
[Byte] [Esa]
00000000 = 00
00000001 = 01
00001111 = 0F
00010000 = 10
11111111 = FF
Che cosa sono i numeri
Nell'ambito informatico capire che cosa sono i numeri è fondamentale per comprendere i sistemi di numerazione.
Tutti i numeri indipendentemente dal sistema di numerazione scelto indicano quantità di unità oppure di cose.
Ad esempio, il numero 9 decimale potrebbe indicare un insieme di nove auto:

Per indicare un insieme di nove auto in ottale il numero sarebbe 11, mentre in binario sarebbe 1001.
Come mai numeri diversi indicano la stessa quantità di cose?
Per rispondere a questa domanda dobbiamo capire che cos'è il sistema posizionale.
Il sistema posizionale
Il sistema posizionale definisce le regole da applicare per capire la quantità di unità oppure cose indicata da un numero.
Prima di tutto è importante definire il sistema di numerazione usato per scrivere i numeri, perché in questo modo possiamo conoscere il numero di cifre disponibili.
Il numero di cifre usate da un sistema di numerazione si chiama base, ad esempio la base del sistema decimae è uguale a 10 perché usa dieci cifre: 0,1,2,3,4,5,6,7,8,9.
La base del sistema esadecimale è uguale a 16 perché questo sistema usa sedici cifre: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E;F.
Attenzione le cifre A,B,C,D,E,F se le trovate in un calcolo valogno rispettivamente: 10,11,12,13,14,15.
Per capire a quale sistema di numerazione appartiene un numero, basta indicare la base come pedice, come mostra l'esempio seguente:
910
118
10012
Tutti e tre i numeri indicano 9 unità.
La prima regola del sistema posizionale ci dice che le cifre di un numero possono indicare quantità di unità diverse in base alla loro posizione nel numero; per questo motivo si parla di sistema posizionale.
Per conoscere la quantità di unità indicata da ogni cifra in un numero, bisogna moltiplicare le cifra per un valore detto peso. I valori dei pesi cambiano in base alla posizione della cifra nel numero e in base al sistema di numerazione usato.
Per ottenere i valori dei pesi corrispondenti alle posizioni delle cifre in un numero, basta calcolare la potenza seguente:
base(posizione-1)
dove base indica il numero di cifre del sistema di numerazione usato e posizione indica dove si trova la cifra nel numero.
Per il sistema decimale, la base è 10, quindi i pesi sono i seguenti:
Posizione Base Esponente Peso
1 10 1-1=0 1
2 10 2-1=1 10
3 10 3-1=2 100
4 10 4-1=3 1000
In realtà i pesi del sistema decimale sono le unità (U), le decine (D), le centinaia (C), le migliaia (M), etc., che impariamo a scuola quando facciamo la scomposizione dei numeri.
Per il sistema binario, la base è 2, quindi i pesi sono i seguenti:
Posizione Base Esponente Peso
1 2 1-1=0 1
2 2 2-1=1 2
3 2 3-1=2 4
4 2 4-1=3 8
5 2 5-1=4 16
6 2 6-1=5 32
7 2 7-1=6 64
8 2 8-1=7 128
Per il sistema ottale, la base è 8, quindi i pesi sono i seguenti:
Posizione Base Esponente Peso
1 8 1-1=0 1
2 8 2-1=1 8
3 8 3-1=2 64
4 8 4-1=3 512
Per il sistema esadecimale, la base è 16, quindi i pesi sono i seguenti:
1 16 1-1=0 1
2 16 2-1=1 16
3 16 3-1=2 256
4 16 4-1=3 4096
Adesso che conosciamo i pesi di tutti i sistemi di numerazione, possiamo fare un esempio.
Il numero decimale 255 indica duecentocinquanta cinque unità o cose, come mostra il calcolo seguente:
5 x 1 = 5
5 x 10 = 50
2 x 100 = 200
--------------------
5+50+200=255 unità
Dimostrare che i numeri 111111112 , 3778 e FF16 , indicano lo stesso numero di unità del numero 25510.
Sistema binario: 11111111
1 x 1 = 1
1 x 2 = 2
1 x 4 = 4
1 x 8 = 8
1 x 16 = 16
1 x 32 = 32
1 x 64 = 64
1 x 128 = 128
------------------------
1+2+4+8+16+32+64+128=255 unità
Sistema ottale: 377
7 x 1 = 7
7 x 8 = 56
3 x 64 = 192
------------------------
7+56+192=255 unità
Sistema esadecimale: FF
In questo caso per fare una verifica dovete ricordare che le cifre esadecimali A, B, C, D, E, F, corrispondono ai numeri seguenti:
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15
Quindi
F x 1 = 15 x 1 = 15
F x 16 = 15 x 16 = 240
------------------------
15+240=255 unità
Come si convertono i numeri decimali in numeri binari, ottali ed esadecimali
Per convertire un numero decimale nel numero corrispondente ad un sistema di numerazione diverso, basta procedere nel modo seguente:
1) Definire la base del sistema di numerazione in cui volete convertire il numero decimale;
2) Dividere il numero decimale per la base del sistema di numerazione scelto fino a quando è possibile;
3) Infine, prendere l'ultimo risultato ottenuto, insieme ai resti di tutte le divisioni fatte e scriverli da sinista verso destra.
Ad esempio, convertiamo il numero decimale 255 in binario, ottale e esadecimale.
1) Sistema binario
base=2, segue:
255/2 = 127 con resto 1
127/2 = 63 con resto 1
63/2 = 31 con resto 1
31/2 = 15 con resto 1
15/2 = 7 con resto 1
7/2 = 3 con resto 1
3/2 = 1 con resto 1
da cui si ottiene che:
25510 = 111111112
2) Sistema ottale
base=8, segue:
255/8 = 31 con resto 7
31/8 = 3 con resto 7
da cui si ottiene che:
25510 = 3778
3) Sistema esadecimale
base=16, segue:
255/16 = 15 con resto 15
da cui si ottiene che:
25510 = 151516 = FF16
Matematica applicata
Laboratorio 1
Creare un programma che calcola i primi otto pesi dei seguenti sistemi di numerazione:
1) Decimale (Dec)
2) Binario (Bin)
3) Ottale (Ott)
4) Esadecimale (Esa)
Soluzione JavaScript
var input = require("readline-sync");
var base = 0;
var nomeSistemaDiNumerazione = "";
var risposta = "";
var scelta = 0;
do {
// Menu per la scelta del sistema di numerazione
console.log("1) Sistema Decimale (Dec)");
console.log("2) Sistema Binario (Bin)");
console.log("3) Sistema Ottale (Ott)");
console.log("4) Sistema Esadecimale (Esa)");
console.log("5) Esci");
scelta = parseInt(input.question("Scegli: "))
// Visualizzo un errore se la scelta non è corretta
while (scelta < 1 || scelta > 5 || isNaN(scelta)) {
console.log("Errore:scegli un numero tra 1 e 5 ...");
scelta = input.question("Scegli: ");
}
// Imposto la base e il nome del sistema di numerazione scelto
if (scelta == 1) {
base = 10;
nomeSistemaDiNumerazione = "Decimale (Dec)";
} else if (scelta == 2) {
base = 2;
nomeSistemaDiNumerazione = "Binario (Bin)";
} else if (scelta == 3) {
base = 8;
nomeSistemaDiNumerazione = "Ottale (Ott)";
} else if (scelta == 4) {
base = 16;
nomeSistemaDiNumerazione = "Esadecimale (Esa)";
}
if (scelta != 5) {
// Calcolo i primi 8 pesi in base al sistema di numerazione scelto
console.log("Pesi delle prime 8 cifre di un numero " + nomeSistemaDiNumerazione);
for (x = 0; x <= 7; x++) {
console.log((x + 1) + ") " + Math.pow(base, x));
}
risposta = input.question("Premi invio per continuare ...");
}
} while (scelta != 5);
console.log("Fine programma");
Soluzione Python
import math
base = 0
nomeSistemaDiNumerazione = ''
risposta = ''
scelta = 0
while scelta != 5:
# Menu per la scelta del sistema di numerazione
print("1) Sistema Decimale (Dec)")
print("2) Sistema Binario (Bin)")
print("3) Sistema Ottale (Ott)")
print("4) Sistema Esadecimale (Esa)")
print("5) Esci")
scelta = int(input("Scegli: "))
# Visualizzo un errore se la scelta non è corretta
while scelta < 1 or scelta > 5:
print("Errore:scegli un numero tra 1 e 5 ...")
scelta = int(input("Scegli: "))
# Imposto la base e il nome del sistema di numerazione scelto
if scelta == 1:
base = 10
nomeSistemaDiNumerazione = 'Decimale (Dec)'
elif scelta == 2:
base = 2
nomeSistemaDiNumerazione = 'Binario (Bin)'
elif scelta == 3:
base = 8
nomeSistemaDiNumerazione = 'Ottale (Ott)'
elif scelta == 4:
base = 16
nomeSistemaDiNumerazione = "Esadecimale (Esa)"
if scelta != 5:
# Calcolo i primi 8 pesi in base al sistema di numerazione scelto
print("Pesi delle prime 8 cifre di un numero " + nomeSistemaDiNumerazione)
for x in range(8):
print(str((x + 1)) + ") " + str(int(math.pow(base, x))))
risposta = input("Premi invio per continuare ...")
print("Fine programma")
Laboratorio 2
Creare un programma che converte un numero decimale in un numero:
1) Binario (Bin)
2) Ottale (Ott)
3) Esadecimale (Esa)
Soluzione JavaScript
var input = require("readline-sync");
var numero = 0;
var numeroDecimale = 0;
var numeroConvertito = "";
var base = 0;
var risultato = 0;
var resto = 0;
var cifre = [];
var cifreNumero = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F'];
var nomeSistemaDiNumerazione = "";
var risposta = "";
var scelta = 0;
do {
cifre = [];
numeroDecimale = parseInt(input.question("Inserisci un numero decimale: "))
while (numeroDecimale < 0 || isNaN(numeroDecimale)) {
console.log("Errore: inserire un numero uguale a zero o mmaggiore di zero ...");
numeroDecimale = parseInt(input.question("Inserisci un numero decimale: "))
}
// Menu per la scelta del sistema di numerazione
console.log("1) Sistema Binario (Bin)");
console.log("2) Sistema Ottale (Ott)");
console.log("3) Sistema Esadecimale (Esa)");
scelta = parseInt(input.question("Scegli il sistema di converione: "))
// Visualizzo un errore se la scelta non è corretta
while (scelta < 1 || scelta > 3 || isNaN(scelta)) {
console.log("Errore:scegli un numero tra 1 e 3 ...");
scelta = parseInt(input.question("Scegli il sistema di conversione: "));
}
// Imposto la base e il nome del sistema di numerazione scelto
if (scelta == 1) {
base = 2;
nomeSistemaDiNumerazione = "Binario (Bin)";
} else if (scelta == 2) {
base = 8;
nomeSistemaDiNumerazione = "Ottale (Ott)";
} else if (scelta == 3) {
base = 16;
nomeSistemaDiNumerazione = "Esadecimale (Esa)";
}
// Converto il numero decimale nel sistema di numerazione scelto
numero = numeroDecimale;
while (numero >= base) {
risultato = Math.floor(numero / base);
resto = numero % base;
cifre.push(resto);
numero = risultato;
}
cifre.push(numero);
// stampo il numero convertito
numeroConvertito = "";
for (var x = cifre.length - 1; x >= 0; x--) {
numeroConvertito = numeroConvertito + cifreNumero[cifre[x]];
}
console.log("Numero decimale da convertire: " + numeroDecimale);
console.log("Numero convertito in " + nomeSistemaDiNumerazione + " " + numeroConvertito);
risposta = input.question("Vuoi convertire un altro numero (s/n) ? ");
while (risposta.toLowerCase() != 's' && risposta.toLowerCase() != 'n') {
console.log("Errore: inserire s oppure n ...");
risposta = input.question("Vuoi convertire un altro numero (s/n) ? ");
}
} while (risposta.toLowerCase() == 's');
console.log("Fine programma");
Soluzione Python
numero = 0
numeroDecimale = 0
numeroConvertito = ''
base = 0
risultato = 0
resto = 0
cifre = []
cifreNumero = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F']
nomeSistemaDiNumerazione = ''
risposta = 's'
scelta = 0
while risposta=='s':
cifre = []
numeroDecimale = int(input("Inserisci un numero decimale: "))
while numeroDecimale < 0:
print("Errore: inserire un numero uguale a zero o mmaggiore di zero ...")
numeroDecimale = int(input("Inserisci un numero decimale: "))
# Menu per la scelta del sistema di numerazione
print("1) Sistema Binario (Bin)")
print("2) Sistema Ottale (Ott)")
print("3) Sistema Esadecimale (Esa)")
scelta = int(input("Scegli il sistema di converione: "))
# Visualizzo un errore se la scelta non è corretta
while scelta < 1 or scelta > 3:
print("Errore:scegli un numero tra 1 e 3 ...")
scelta = int(input("Scegli il sistema di converione: "))
# Imposto la base e il nome del sistema di numerazione scelto
if scelta == 1:
base = 2
nomeSistemaDiNumerazione = 'Binario (Bin)'
elif scelta == 2:
base = 8
nomeSistemaDiNumerazione = 'Ottale (Ott)'
elif scelta == 3:
base = 16
nomeSistemaDiNumerazione = 'Esadecimale (Esa)'
# Converto il numero decimale nel sistema di numerazione scelto
numero = numeroDecimale
while numero >= base:
risultato = int(numero / base)
resto = numero % base
cifre.append(resto)
numero = risultato
cifre.append(numero)
# stampo il numero convertito
numeroConvertito = ""
for x in range(len(cifre)-1,-1,-1):
numeroConvertito = numeroConvertito + cifreNumero[cifre[x]]
print("Numero decimale da convertire: " + str(numeroDecimale))
print("Numero convertito in " + nomeSistemaDiNumerazione + " " + numeroConvertito)
risposta = input("Vuoi convertire un altro numero (s/n) ? ")
while risposta.lower() != 's' and risposta.lower() != 'n':
print("Errore: inserire s oppure n ...")
risposta = input("Vuoi convertire un altro numero (s/n) ? ")
print("Fine programma")
Come eseguire i programmi JavaScript
Per eseguire i programmi JavaScript, bisogna installare il framework node.js sul proprio computer.
Il download del file d'installazione può essere fatto collegandosi al link: https://nodejs.org/it/download/.
Il file di download deve corrispondere al sistema operativo installato sul proprio computer.
Dopo il download eseguire il file per installare node.js.
Per verificare se il framework node.js è stato installato correttamente, dal prompt dei comandi del sistema operativo usato, eseguire il comando:
node --version
dovrebbe essere visualizzata la versione di node.js installata, come mostra l'immagine seguente:

Successivamente bisogna creare una cartella "laboratori" dove salvare i due programmi JavaScript da eseguire.
Per salvare i programmi nella cartella "laboratori", basta copiarli nel blocco note o in qualunque editor di testo e salvarli con i nomi:
1) calcola_pesi.js
2) converti_decimale.js
Infine, da prompt dei comandi, entrare nella cartella laboratori ed eseguire il comando:
npm install readline-sync
Questa libreria serve per permettere l'inserimento di dati da tastiera, quando vengono eseguiti i programmi.
A queso punto si possono eseguire i programmi con il comando node, che è l'interprete JavaScript di node.js, come mostrano gli esempi seguenti:
node calcola_pesi
oppure
node converti_decimale
Come eseguire i programmi Python
Per eseguire i programmi scritti Python, bisogna installare il framework python sul proprio computer.
Il download del file d'installazione può essere fatto collegandosi al link: https://www.python.org/downloads/.
Il file di download deve corrispondere al sistema operativo installato sul proprio computer.
Dopo il download eseguire il file per installare python.
Attenzione, durante l'installazione è importante spuntare l'opzione "Add Python 3.X to PATH:

Per verificare se il framework python è stato installato correttamente, dal prompt dei comandi del sistema operativo usato, eseguire il comando:
python --version
dovrebbe essere visualizzata la versione di python installata, come mostra l'immagine seguente:

Successivamente bisogna creare una cartella "laboratori" dove salvare i programmi python da eseguire.
Per salvare i programmi nella cartella "laboratori", basta copiarli nel blocco note o in qualunque editor di testo e salvarli con il nomi:
1) calcola_pesi.py
2) converti_decimale.py
Infine, per eseguire i programmi, da prompt dei comandi, entrare nella cartella laboratori ed il comando:
python calcola_pesi.py
oppure
python converti_decimale.py
Leggi anche le altre lezioni ...
COMPETENZE PER PROGRAMMARE:
2-Mondo reale e Mondo Digitale
3-La reppresentazione digitale dei numeri interi e decimali
4-Le stringhe
5-Le espressioni regolari (REGEXP)
6-Date, ore e fusi orari
Segui sul canale YouTube "Skill Factory Channel" la Playlist: COMPETENZE PER PROGRAMMARE
TUTORIALS
1-Laboratori di logica di programmazione in C
2-Impariamo a programmare con JavaScript
3-Ricominciamo dal linguaggio SQL
4-Introduzione alla logica degli oggetti
5-TypeScript
6-Impariamo a programmare in Python
7-Come sviluppare un sito in WordPress
PAR GOL (Garanzia di Occupabilità dei Lavoratori)

Se sei residente in Campania e cerchi lavoro, sai che puoi partecipare gratuitamente ad un corso di formazione professionale PAR GOL?
I corsi di formazione professionale PAR GOL sono finanziati dalla Regione Campania e ti permettono di acquisire una Qualifica Professionale Europea (EQF) e di partecipare ad un tirocinio formativo aziendale.
Invia il tuo CV o una manifestazione d'interesse a: recruiting@skillfactory.it
oppure
chiama ai seguenti numeri di telefono:
Tel.: 081/18181361
Cell.: 327 0870141
oppure
Contattaci attraverso il nostro sito: www.skillfactory.it
Per maggiori informazioni sul progetto PAR GOL, clicca qui.
Per maggiori informazioni sulle Qualifiche Professionali Europee (EQF), clicca qui.
Academy delle professioni digitali
Per consultare il catalogo dei corsi online della nostra Academy ...

... collegati al nostro sito: www.skillfactory.it





 Le Tue Aule
Le Tue Aule
 I Tuoi Gruppi
I Tuoi Gruppi
 Le Tue Selezioni
Le Tue Selezioni



 Scheda Azienda
Scheda Azienda