Skill Factory
Categoria: Tutorials
Come progettare e sviluppare giochi per l'educazione e la formazione con Python: lezione 5
![]() Mirko Onorato |
Mirko Onorato |
 Skill Factory - 23/09/2024 08:30:04 | in Tutorials
Skill Factory - 23/09/2024 08:30:04 | in Tutorials
 In questa lezione completiamo la prima esperienza di matematica di Hammer-XP, implementando tutti i livelli di gioco previsti:
In questa lezione completiamo la prima esperienza di matematica di Hammer-XP, implementando tutti i livelli di gioco previsti:
1) Elimina dall'area di gioco i numeri pari;
2) Elimina dall'area di gioco 3 e i multipli di 3;
3) Elimina dall'area di gioco 7 e i numeri divisibili per 7;
4) Elimina dall'area di gioco i numeri primi.
I livelli sono stati progettati per ragazzi delle scuole elementari, che hanno un'età massima di 10 anni.

I quattro livelli sono stati implementati attraverso le funzioni seguenti:
1) def exp_01_01(block_list,sprite_list,game_exit,scheda);
2) def exp_01_02(block_list,sprite_list,game_exit,scheda);
3) def exp_01_03(block_list,sprite_list,game_exit,scheda);
4) def exp_01_04(block_list,sprite_list,game_exit,scheda).
Puoi consultare il codice delle funzioni, scaricando il programma Python nel file zip alla fine di questa lezione.
Il primo livello parte subito all'avvio del gioco, con la funzione:
def exp_01_01(block_list,sprite_list,game_exit,scheda).
L'avvio degli altri livelli viene gestito attraverso la variabile level_progressivo e la struttura condizionale seguente:
level_progressivo+=1
if level_progressivo==2:
exp_01_02(block_list,sprite_list,game_exit,scheda)
elif level_progressivo==3:
exp_01_03(block_list,sprite_list,game_exit,scheda)
elif level_progressivo==4:
exp_01_04(block_list,sprite_list,game_exit,scheda)
Per passare al livello seguente è stato aggiunto il pulsante "START NEXT LEVEL >>":
bloccoGoalNextLevel=Etichetta((201,55,184),300,40,500,164,'START NEXT LEVEL >>')
Quando Hammer tocca il pulsante START NEXT LEVEL >>", si passa al livello successivo.
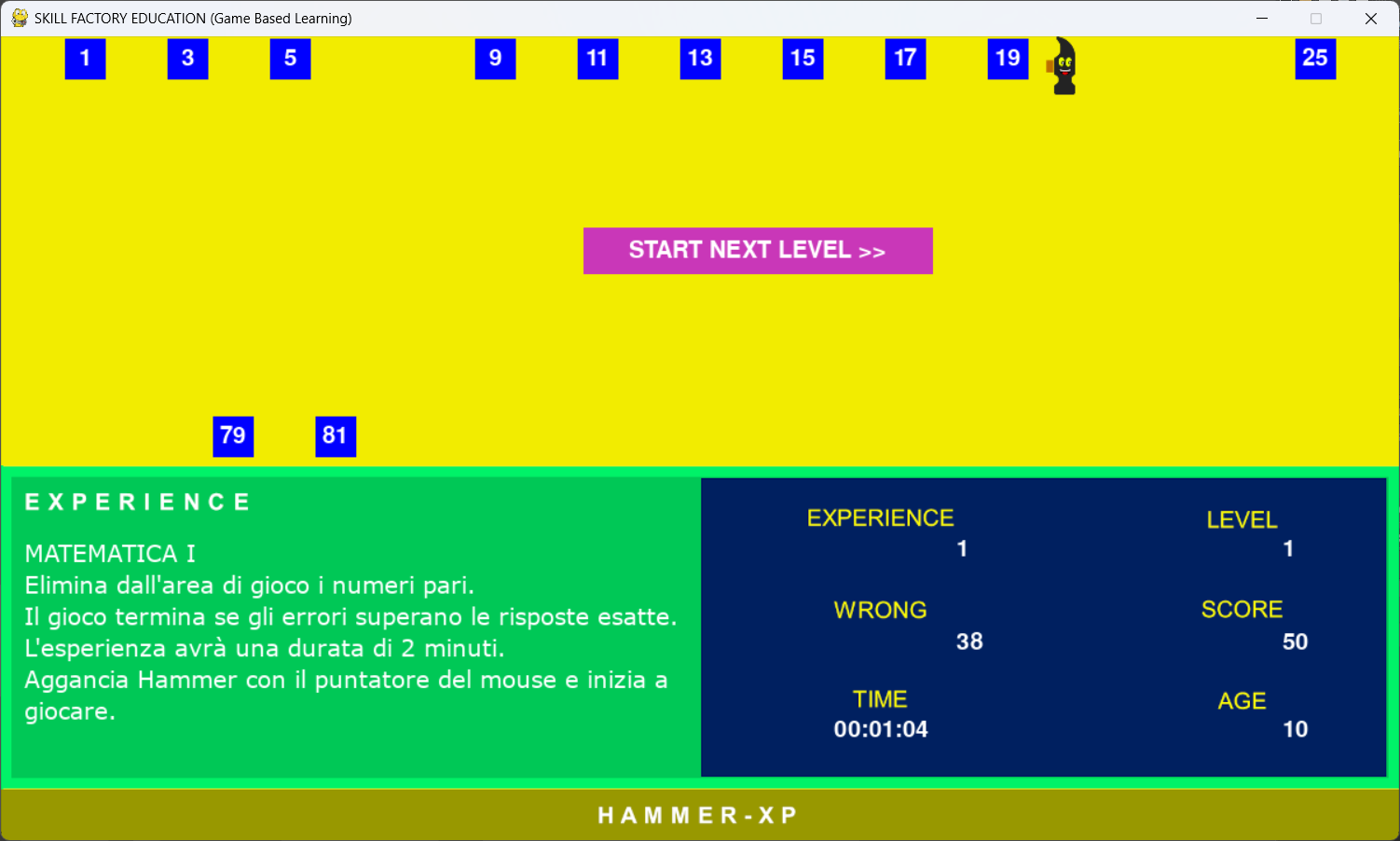
Il suono per accedere al prossimo livello è stato creato con la funzione seguente:
def beep_next_level():
frequenza=150
durata=[200,75,100,125,350,500,700]
for x in range(5):
winsound.Beep(frequenza,durata[x])
frequenza+=150
winsound.Beep(frequenza,1000)
FASI DEL GIOCO
All'avvio, il gioco presenta subito il primo livello, dove bisogna eliminare tutti i numeri pari.
Il gioco finisce se termina il tempo a disposizione oppure gli errori (wrong) superano i successi (score).
Quando il gioco termina appare il pulsante "GAME OVER", come mostra l'immagine seguente:
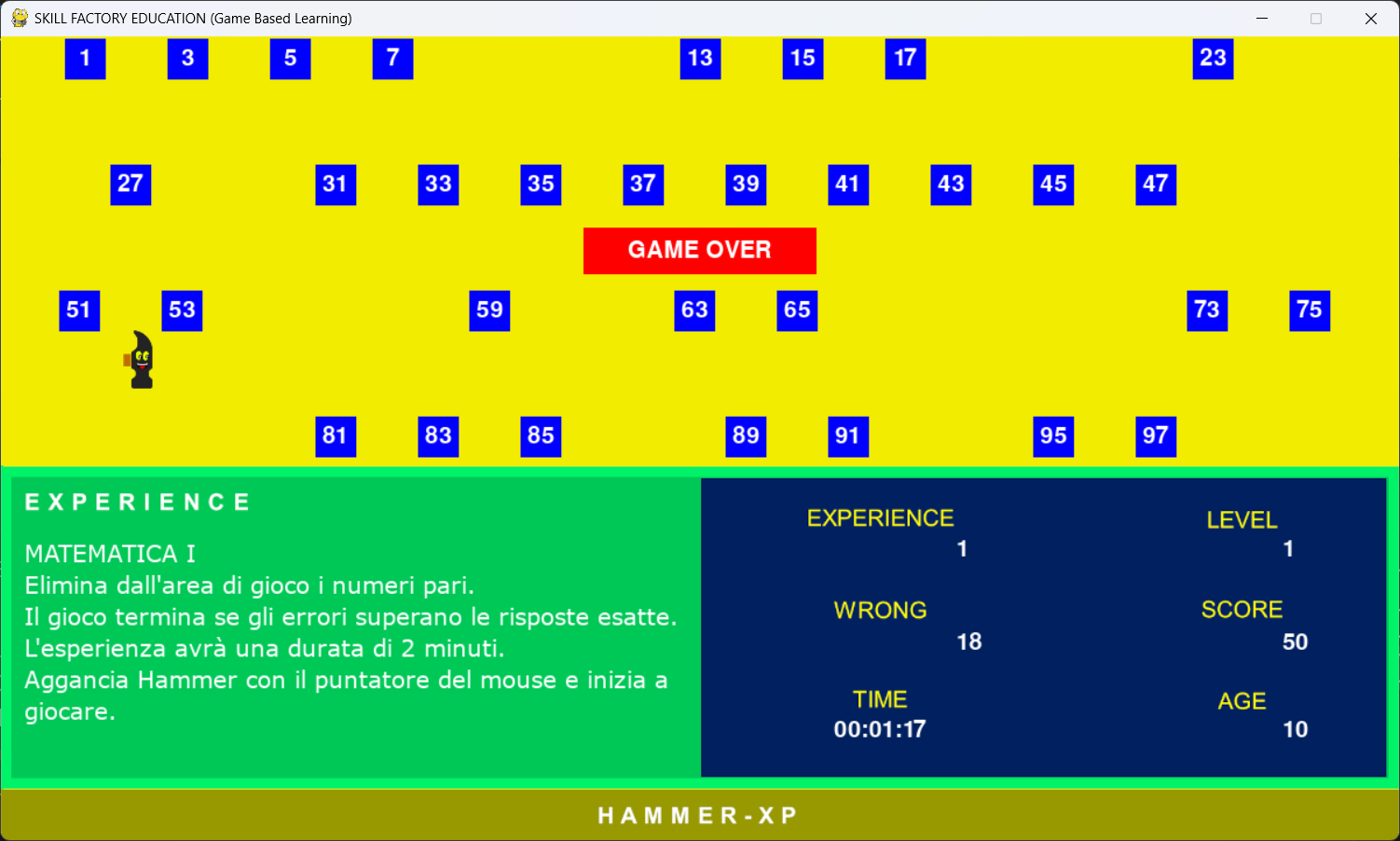
Se il giocatore elimina dall'area di gioco tutti i numeri pari passa al livello successivo.
Il secondo livello prevede che il giocatore deve eliminare dall'area di gioco il 3 e i multipli di 3. Anche in questo caso il gioco finisce se termina il tempo a disposizione oppure gli errori (wrong) superano i successi (score).
Il terzo livello è simile al secondo, ma qui il giocatore deve eliminare dall'area di gioco il 7 e i numeri divisibili per 7.
Infine, il quarto livello è quello più difficile, perché il giocatore deve eliminare dall'area di gioco tutti i numeri primi; quindi, prima d'iniziare a giocare, è il caso di studiare bene l'argomento.
Se il giocatore, termina con successo anche l'ultimo livello, appare il pulsante "GOAL!!!"

Tutte le fasi del gioco vengono gestite con il codice Python seguente:
if not gameNextLevel:
blocks_hit_list = pygame.sprite.spritecollide(hammer, block_list, True)
t2=time.time()
t_value=math.floor(t2-t1)
for blocco in blocks_hit_list:
if blocco.hit:
score_value+=1
else:
wrong_value+=1
if score_value==game_exit.score_value_exit and level_progressivo<4:
gameNextLevel=True
block_level.add(bloccoGoalNextLevel)
sprite_list.add(bloccoGoalNextLevel)
beep_next_level()
elif score_value==game_exit.score_value_exit and level_progressivo==4:
gameOver=True
sprite_list.add(bloccoGoal)
beep_goal()
elif wrong_value>score_value or t_value==game_exit.t_value_exit:
gameOver=True
sprite_list.add(bloccoGameOver)
beep_game_over()
COME ESEGUIRE IL GIOCO
Per eseguire il gioco HAMMER-XP dovete installare il framework Python sul vostro computer.
Per eseguire il download del setup per installare Python clicate qui oppure collegatevi al link seguente: https://www.python.org/downloads/.
Dopo il download del setup, eseguitelo per installare Python.
Attenzione, durante l'installazione è importante spuntare l'opzione "Add Python 3.X to PATH:
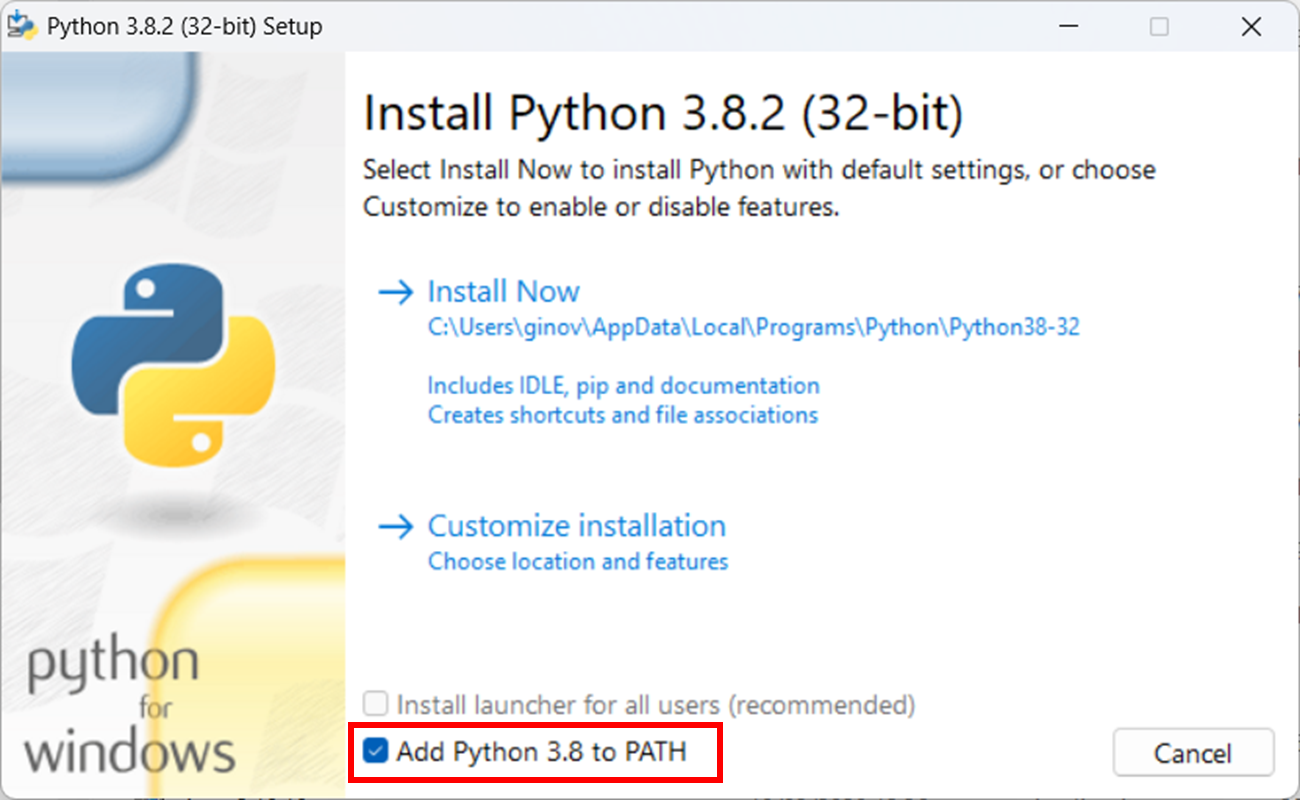
Dopo che avete impostato l'opzione, cliccate sul comando Install Now.
Per verificare se il framework Python è stato installato correttamente, dal prompt dei comandi del sistema operativo, eseguite il comando:
python --version
Se l'installazione è andata a buon fine viene visualizzata la versione di Python, come mostra l'immagine seguente:
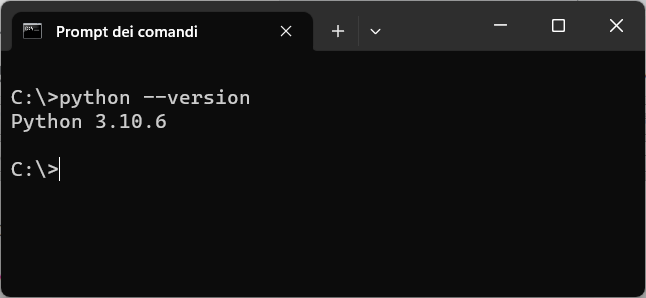
Successivamente create una cartella "HAMMER-XP" e in questa cartella estraete il contenuto del file zip che contiene le risorse del gioco.
Per avviare il gioco dal prompt dei comadi, entrate nella cartella hammer-xp, ed eseguite il comando:
python hammer_experience_matematica_001_V02.py
Nella prossima lezione implementeremo l'esperienza d'italiano per imparare a riconoscere i sostantivi, gli aggettivi, i verbi e gli avverbi.
Per il download delle risorse di questa lezione cliccate qui.
< LEZIONE PRECEDENTE | VAI ALLA PRIMA LEZIONE
T U T O R I A L S S U G G E R I T I
- Competenze per programmare
- Impariamo Python giocando al "Solitario del ferroviere"
- Impariamo a programmare con JavaScript
- Laboratori di Logica di programmazione in C
- Introduzione alla Logica degli oggetti
- Ricominciamo ... dal Linguaggio SQL
- APP Mania
- Come sviluppare un Sito con Wordpress
PER IMPARARE A PROGRAMMARE, SEGUI LE PLAYLIST SUL NOSTRO CANALE YOUTUBE "SKILL FACTORY CHANNEL": clicca qui per accedere alle playlist
PAR GOL (Garanzia di Occupabilità dei Lavoratori)

Se sei residente in Campania e cerchi lavoro, sai che puoi partecipare gratuitamente ad un corso di formazione professionale PAR GOL?
I corsi di formazione professionale PAR GOL sono finanziati dalla Regione Campania e ti permettono di acquisire una Qualifica Professionale Europea (EQF) e di partecipare ad un tirocinio formativo aziendale.
Invia il tuo CV o una manifestazione d'interesse a: recruiting@skillfactory.it
oppure
chiama ai seguenti numeri di telefono:
Tel.: 081/18181361
Cell.: 327 0870141
oppure
Contattaci attraverso il nostro sito: www.skillfactory.it
Per maggiori informazioni sul progetto PAR GOL, clicca qui.
Per maggiori informazioni sulle Qualifiche Professionali Europee (EQF), clicca qui.
Academy delle professioni digitali
Per consultare il catalogo dei corsi online della nostra Academy ...

... collegati al nostro sito: www.skillfactory.it

... collegati al nostro sito: www.skillfactory.it
6. Competenze per programmare: date, ore e fusi orari
![]() Gino Visciano |
Gino Visciano |
 Skill Factory - 16/08/2024 11:59:36 | in Tutorials
Skill Factory - 16/08/2024 11:59:36 | in Tutorials
Il tempo sulla Terra non è assoluto, ma relativo, quindi la sincronizzazione delle date e delle ore, nell'era della globalizzazione, può diventare una cosa complicata se non sono chiari alcuni concetti.
Il primo concetto fondamentale per gestire le date è il formato della data, perché ogni nazione o sistema informatico può adottare delle regole diverse.
I formati data più utilizzati dai sistemi informatici sono i seguenti:
1) MM/dd/yyyy;
2) yyyy/MM/dd;
3) dd/MM/yyyy.
MM=mese
yyyy=anno
2) yyyy-MM-dd;
3) dd-MM-yyyy.
Esempio 1
Inserire una data di tipo stringa, nel formato dd/MM/yyyy.
Estrarre la data il giorno, il mese e l'anno in forma numerica e stamparli.
Utilizzare il giorno, il mese e l'anno estratti per creare una data di tipo oggetto.
Dalla data di tipo oggetto estrarre la data il giorno, il mese e l'anno in forma numerica e stamparli.
Infine, utilizzando la data di tipo oggetto stampare le date nei formati seguenti:
1) MM-dd-yyyy;
2) yyyy-MM-dd;
3) dd-MM-yyyy.
2) moment
npm install moment
Esempio 2
Creare un vettore con 5 date di tipo stringa.
Le date devono essere inserite nel formato dd/MM/yyyy.
Stampare le date in ordine crescente.
Soluzione Python:
Clicca qui per visualizzare la soluzione.
Soluzione JavaScript (node.js):
Clicca qui per visualizzare la soluzione.
Esempio 3
Creare un vettore con 5 oggetti di tipo data.
Le date devono essere inserite nel formato dd/MM/yyyy.
Stampare le date in ordine crescente.
Soluzione Python:
Clicca qui per visualizzare la soluzione.
Soluzione JavaScript (node.js):
Clicca qui per visualizzare la soluzione.
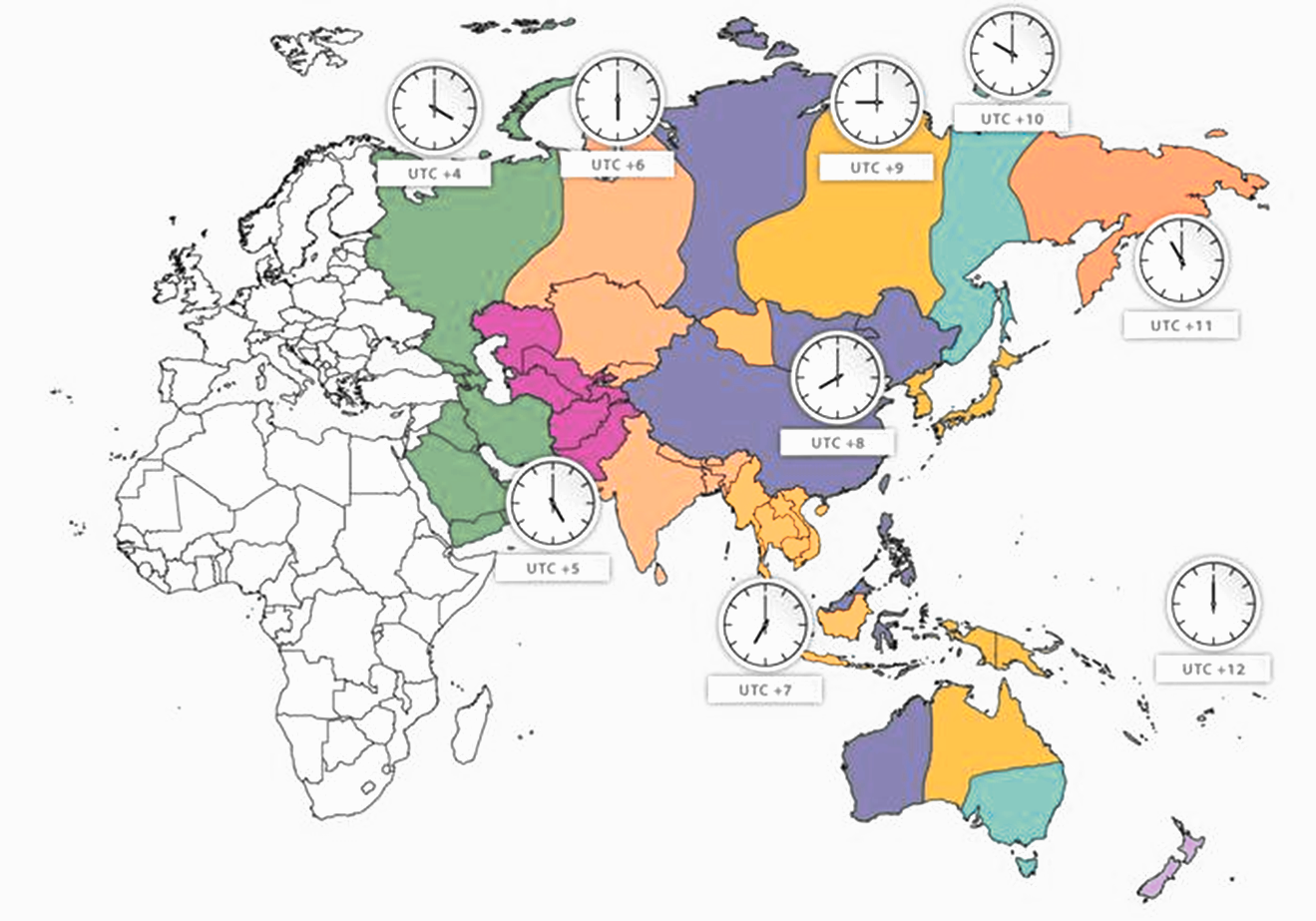
Un altro concetto importante è quello di fuso orario, perché permette di sincronizzare l'ora degli eventi tra località molto distanti tra loro. L'ora locale di una località cambia in base alla longitudine in cui si trova, per questo motivo il tempo sulla Terra non è assoluto, ma è relativo; attraverso i fusi è possibile conoscere la differenza di orario che esiste tra due località diverse.
Per essere sicuri di quando riceverete la telefonata del vostro amico, dovete chiarire tre cose:
1) il formato della data indicata;
2) la città a cui fa riferimento l'ora indicata;
3) se è in vigore l'ora legale
In questo caso il problema dell'ora legale non c'è perché sia in America che in Italia va in vigore a marzo e termina a fine ottobre; quindi, l'ora legale non avrà nessun effetto sul fuso orario.
Allora vediamo quali sono gli altri casi possibili:
A. Data espressa in formato Europeo (dd/MM/yyyy) e ora di Roma
Questo è il caso più semplice, perché la telefonata del vostro amico di New York dovrebbe arrivare il 10 maggio 2024 alle ore 11:00.
B. Data espressa in formato Europeo (dd/MM/yyyy) e ora di New York
In questo caso c'è il problema del fuso orario tra Roma e New York. La longitudine (meridiano) di New York è diversa da quella della città di Roma, quindi, l'ora di New York è di 6 ore indietro rispetto a quella di Roma.
A causa del fuso orario, la telefonata del vostro amico di New York dovrebbe arrivare il 10 maggio 2024 alle ore 17:00.
C. Data espressa in formato USA (MM/dd/yyyy) e ora di Roma
In questo caso considerando il formato USA della data e il fuso orario di New York, otteniamo che la telefonata del vostro amico di New York dovrebbe arrivare il 5 ottobre 2024 alle ore 17:00.
I sistemi informatici, per allineare le date e le ore tra località del mondo con longitudine diversa, usano le informazioni di Time zone, da cui si può ottenere il fuso orario e se è in vigore o meno l'ora legale.
Esempio 4
Stampare l'ora corrente di Roma.
Estrarre ore, minuti e secondi e stamparli.
Stampare il fuso orario con Greenwich.
Soluzione Python:
Clicca qui per visualizzare la soluzione.
Soluzione JavaScript (node.js):
Clicca qui per visualizzare la soluzione.
Esempio 5
Stampare la data e l'ora corrente e le informazioni di Time zone di Roma e di New York.
Soluzione Python:
Clicca qui per visualizzare la soluzione.
Soluzione JavaScript (node.js):
Clicca qui per visualizzare la soluzione.
COME MISURIAMO IL TEMPO SULLA TERRA
La misura del tempo sulla Terra è una questione di giri ... Per questo motivo il tempo si misura in sessagesimi (sistema di misura in base 60).
Un giorno corrisponde al tempo impiegato dalla Terra per compiere un giro completo di 360°, intorno al proprio asse.
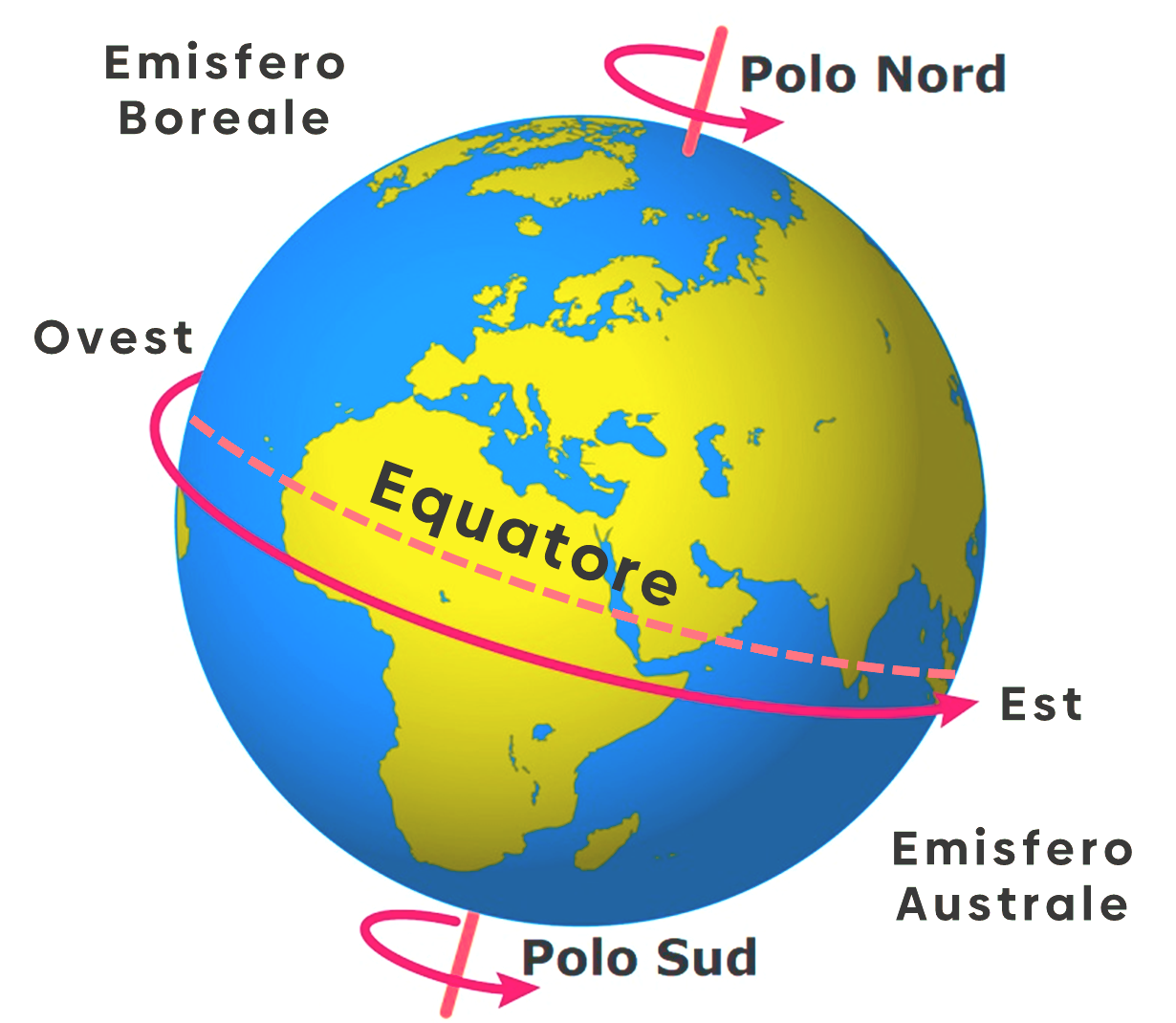
La Terra ruota in senso antiorario, da ovest (occidente/ponente) verso est (oriente/levante); per ogni ora che passa ruota di 15°, per questo motivo un giorno è composto da circa 24 ore, come mostra la formula seguente:
360° / 15° = 24 ore.
In base al sistema sessagesimale, le unità sono rappresentate dai secondi (simbolo ''). Ogni sessanta secondi s'incrementano di 1 i minuti (simbolo '). Ogni sessanta minuti s'incrementano di 1 le ore.
Per questo motivo il tempo sulla Terra si indica nel formato:
ore:minuti:secondi
oppure
hh:mm:ss
1 ora (rotazione Terra di 15°) = 60 minuti (60')
1 minuto (rotazione Terra di 0,25°) = 60 secondi (60'')
Quindi
1 ora = 60' = 3600''
1 giorno = 24 ore = 1440' = 86400''
Anche le lancette dell'orologio analogico, con cui misuriamo il tempo, girano.
Un orologio non è altro che un contatore sessagesimale.
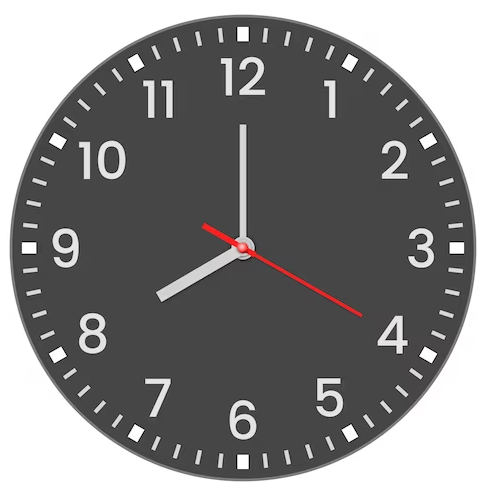
Per ogni giro completo (360°) della Terra intono al proprio asse, che si completa in circa 24 ore:
1) la lancetta dei secondi ruota intorno al quadrate dell'orologio per 1440 volte.
2) la lancetta dei minuti ruota intorno al quadrate dell'orologio per 24 volte;
1) la lancetta delle ore ruota intorno al quadrate dell'orologio per 2 volte;
Esempio 6
Visualizzare le seguenti informazioni sulla rotazione della Terra:
1) Data e ora di Greenwich con fuso orario
2) Data e ora di Roma con fuso orario
3) Differenza di fuso orario tra Roma e Greenwich
4) Percentuale di rotazione della Terra prima di completare un giro
5) Percentuale di rotazione della Terra per completare un giro
Soluzione Python:
Clicca qui per visualizzare la soluzione.
Soluzione JavaScript (node.js):
Clicca qui per visualizzare la soluzione.
LATITUDINE E LONGITUDINE
La posizione di qualunque località o punti sulla Terra si può indicare attraverso due coordinate chiamate: Latitudine e Longitudine.
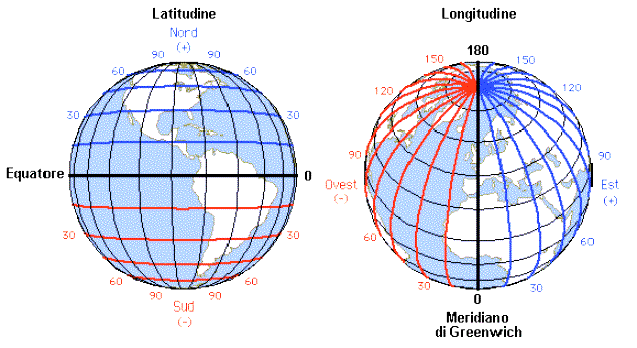
Ad esempio, la città di Roma ha le seguenti coordinate:
Latitudine: 41°53′57.12″ nord
Longitudine: 12°32′42.00″ est.
Mentre la città di Brasilia ha le seguenti coordinate:
Latitudine: 15°46′46″ sud
Longitudine: 47°55′46″ ovest
Potete immaginare la latitudine come il cerchio perpendicolare all'asse terrestre e parallelo all'equatore che passa per una località specifica. Per convenzione la latitudine è Nord se il cerchio si trova nella parte tra l'equatore e il polo Nord (emisfero Boreale), altrimenti è Sud, se il cerchio si trova tra l'equatore e il polo Sud (emisfero Australe).
I cerchi che indicano le latitudini da 0° a 90°, distanziati di 1° l'uno dall'altro, sono detti paralleli. Si contano 90 paralleli a Nord e 90 a Sud.
il parallelo 0 coincide con l'equatore, quindi in totale i paralleli sono 181. Sulle mappe si indica un parallelo solo ogni 15°, quindi ci sono 12 paralleli a Nord e 12 a Sud, oltre l'equatore naturalmente.
Allo stesso modo, potete immaginare la longitudine come un semicerchio parallelo all'asse terrestre e perpendicolare all'equatore che unisce il polo Nord con il polo Sud e passa per una località specifica.
I semicerchi che indicano le longitudini, distanziati di 1° l'uno dall'altro, sono detti meridiani. I meridiani sono 360; quello più importante è il meridiano 0.
Verso la fine del 1800, i Paesi più importanti del mondo, decisero che il meridiano 0 dovesse essere quello che passava per Greenwich, un distretto di Londra in Inghilterra, sulle sponde del fiume Tamigi. Per convenzione le località a destra del meridiano 0 hanno longitudine Est, quelle a sinistra hanno longitudine Ovest.
Sulle mappe si indica un meridiano ogni 15°, quindi ci sono solo 24 meridiani identificati con i numeri da 0 a 23. Questi meridiani sono anche detti meridiani orari, perché a causa della rotazione della Terra, ciascun meridiano, partendo da quello 0 a quello 23, incontra il Sole alle ore 12:00:00, dopo ogni ora.
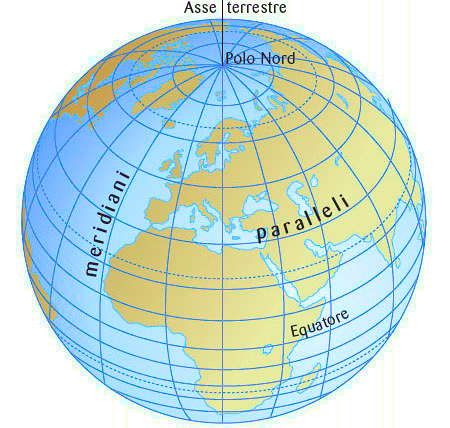
I meridiani orari permettono di definire i fusi orari, fondamentali per stabilire l'ora locale di ogni località del mondo.
Esempio 7
Inserire la latitudine e la longitudine di una località e indicare tra quali paralleli e quali meridiani si trova.
Soluzione Python:
CHE COS'E' IL FUSO ORARIO
Quando parliamo di misura del tempo sulla Terra, dobbiamo ricordare che non sono importanti i paralleli (cerchi paralleli all'equatore, con latitudine da 1 a 90 gradi dell'emisfero Nord e Sud), ma sono fondamentali i meridiani (i 360 semicerchi che unisco, il polo Nord con il polo Sud, a 1° di longitudine l'uno dall'altro), in particolare quelli orari (i 24 meridiani a 15° di longitudine l'uno dall'altro), perché permettono di determinare i fusi orari che servono per calcolare l'ora locale di qualunque località del mondo.
Sappiamo che un giorno corrisponde al tempo impiegato dalla Terra per compiere un giro completo di 360° intorno al proprio asse. Il problema è che le località del mondo si trovano in posizioni diverse; quindi, per misurare il tempo sulla Terra è importante scegliere una località specifica, da usare come riferimento.
Per convenzione si è deciso di utilizzare come località di riferimento per misurare il tempo sulla Terra il distretto di Greenwich, che corrisponde al meridiano zero o longitudine zero. Il tempo s'inizia a contare quando questa località incontra il Sole (punto fisso della volta celeste) alle ore 12:00:00.
Ogni volta che Greenwich compie un giro completo, sul nostro Pianeta sarà trascorso un giorno. Quindi l'ora locale di Greenwich, detta anche Greenwich Mean Time, abbreviato in GMT, è l'ora di riferimento da cui partire per calcolare le ore locali delle altre località del mondo, utilizzando i fusi orari.
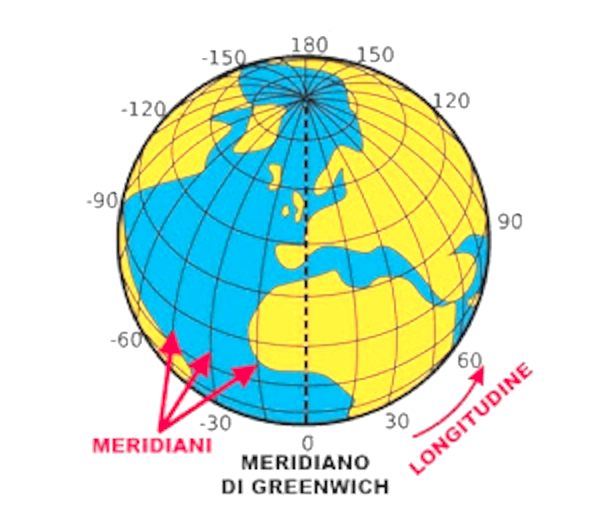
Per ottenere l'ora locale di qualunque località del mondo basta usare la formula seguente:
OL = GMT + FO
OL=ora locale della località in esame
GMT=Greenwich Mean Time
FO=Fuso orario della località in esame (Attenzione i fusi ad ovest del meridiano 0 sono negativi, quelli ad est sono positivi).
Naturalmente il fuso orario di Greenwich, che coincide con il meridiano 0, è uguale a zero.
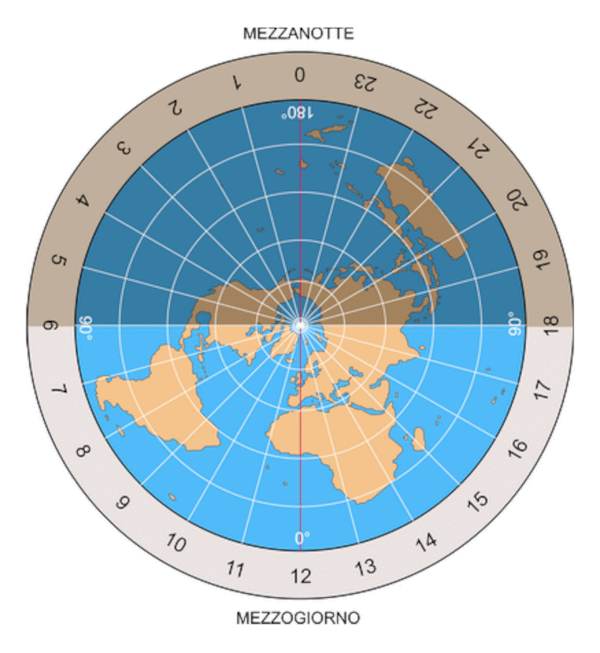
Il valore del fuso orario aumenta di un'ora (+) ogni volta che s'incontra un nuovo meridiano orario, se si procede verso Est del meridiano 0. Altrimenti diminuisce di un'ora (-) ogni volta che s'incontra un nuovo meridiano orario, se si procede verso Ovest del meridiano 0, come mostra l'immagine seguente:
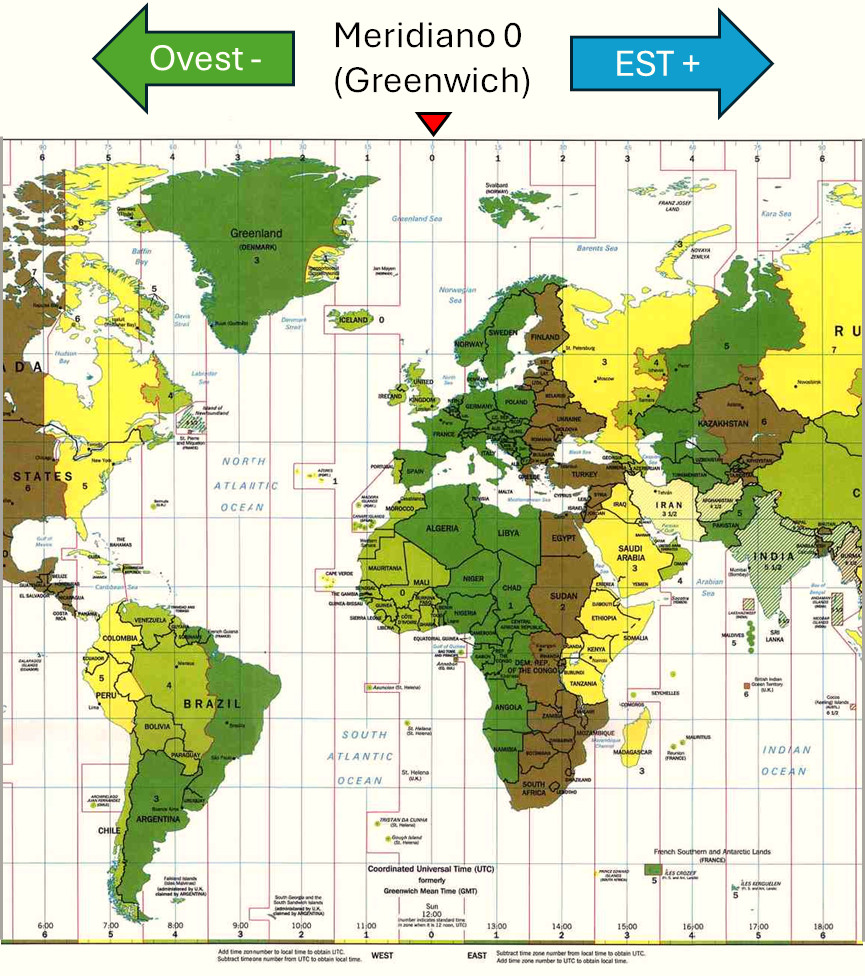
Ad esempio, quando a Greenwich sono le 12:00 a Roma sono le 13:00, perché Roma si trova sul primo meridiano orario ad Est, di Greenwich, dove il fuso orario è uguale a +1. Anche a Parigi sono le 13:00, perché Roma e Parigi, hanno latitudini diverse, ma si trovano sulla stessa longitudine, quindi si trovano sullo stesso meridiano orario e il fuso orario è uguale.
L'Islanda, si trova sul primo meridiano orario ad Ovest di Greenwich; in questo caso il valore del fuso orario è uguale a -1. Quindi quando a Greenwich sono le 12:00, in Islanda sono le 11:00.
La differenza tra i fusi orari di due località diverse, ci permette di conoscere le ore di differenza che ci sono tra le loro ore locali. Ad esempio, il fuso orario di Roma è +1, mentre quello di New York è -5. Questo significa che tra l'ora locale di Roma e quella di New York c'è una differenza di:
-5 - (+1) = -6 ore.
Quindi, quando a Roma sono le 12:00, a New York sono le 6:00 del mattino.
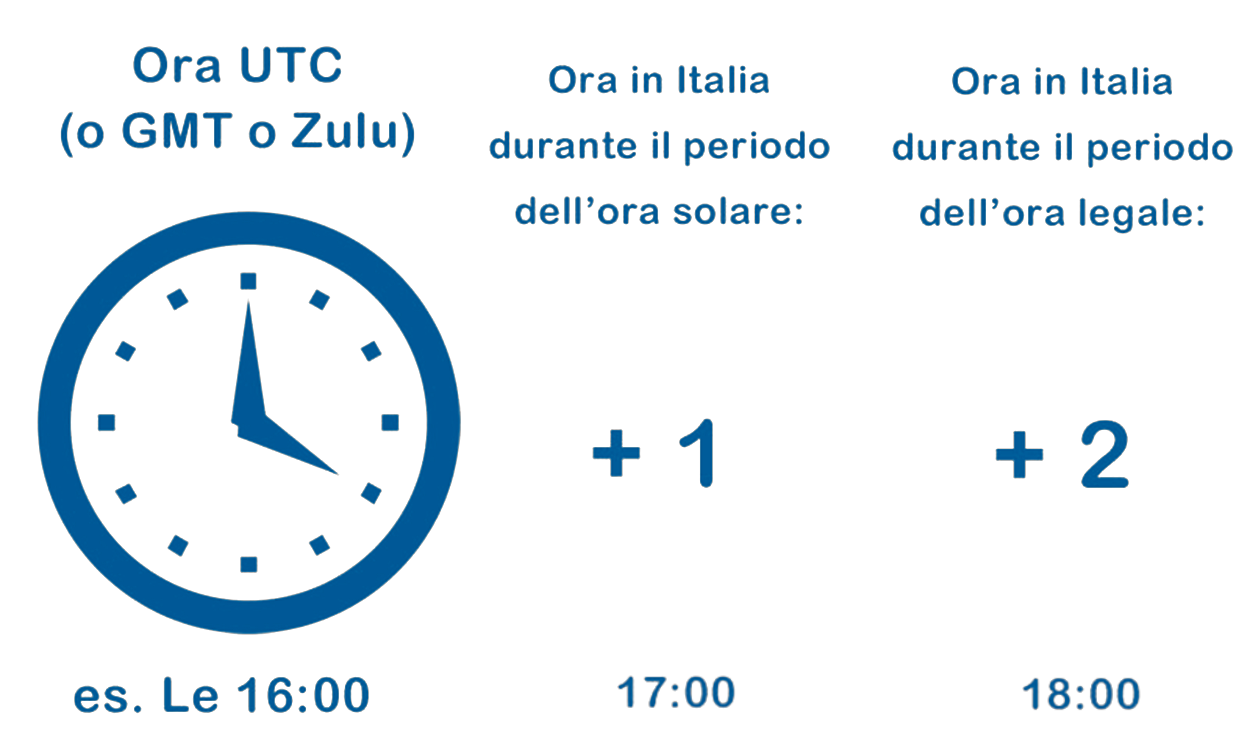
DIFFERENZA TRA GMT E UTC
Il Tempo medio di Greenwich (GMT), come abbiamo visto è il tempo a cui bisogna far riferimento per calcolare l'ora locale di qualunque località del mondo utilizzando i fusi orari. Il GMT non è preciso perhcé è basato su fenomeni celesti e con il tempo deve essere corretto.
Oggi il GMT è stato sostituito dal Tempo Coordinato Universale (Coordinated Universal Time - UTC), conosciuto anche come tempo civile. Il nuovo nome è stato coniato per non dover menzionare una specifica località in uno standard internazionale. L'UTC si basa su misurazioni condotte da orologi atomici, quindi è molto più preciso del GMT.
A causa delle oscillazioni nella velocità di rotazione della Terra (il fenomeno è dovuto soprattutto alla gravità degli altri pianeti), il GMT ritarda costantemente rispetto al "tempo atomico" UTC. Il ritardo è mantenuto entro 0,9 secondi, aggiungendo o togliendo un secondo ad UTC alla fine del mese quando necessario, convenzionalmente il 30 giugno o il 31 dicembre. Il secondo extra, detto intercalare è determinato dall'International Earth Rotation and Reference Systems Service (IERS), basandosi sulle loro misurazioni della rotazione terrestre.
L'UTC è un problema per i sistemi informatici che memorizzano le date come il numero di secondi passati rispetto ad una data antecedente, come ad esempio il sistema operativo Unix, che memorizza la data come il numero di secondi passati dal 1° gennaio 1970. In questi casi diventa impossibile determinare la rappresentazione di una data futura, a causa dei secondi che potrebbero essere stati inseriti o sottratti nel frattempo.
L'UTC è il tempo usato per molti standard Internet e nel World Wide Web. In particolare, il Network Time Protocol è progettato come un modo per distribuire dinamicamente il tempo UTC attraverso Internet.
Il fuso orario UTC è a volte indicato dalla lettera 'Z', per scopi militari, meteorologici, di navigazione aeronavale militare e civile. Poiché l'alfabeto fonetico della NATO e dei radioamatori usa la parola "Zulu" per 'Z', UTC è a volte chiamato "tempo" o "orario Zulu".
Per ottenere l'ora locale di qualunque località del mondo, attraverso l'UTC, basta usare la formula seguente:
OL = UTC + FO
OL=ora locale della località in esame
UTC=Coordinated Universal Time
FO=Fuso orario della località in esame (Attenzione i fusi ad ovest del meridiano 0 sono negativi, quelli ad est sono positivi).
Esempio 8
Visualizzare la data e l'ora corrente e le informazioni di tutti i Time zone del mondo.
Soluzione Python:
Clicca qui per visualizzare la soluzione.
Soluzione JavaScript (node.js):
Clicca qui per visualizzare la soluzione
LO STANDARD ISO 8601
Per indicare le date e le ore in modo univoco in tutto il mondo, è stato creato lo standard ISO 8601. In Europa questo standard è anche conosciuto come EN 28601.
Lo scopo della norma ISO 8601, è quello di fornire indicazioni per i formati numerici di date e orari.
Secondo questo standard le data vanno espresse nel formato anno-mese-giorno, mentre gli orari nel formato ore-minuti-secondi. Tutte le indicazioni di orari, date o intervalli di tempo conformi alla norma ISO vengono indicati con una successione precisa: cominciano con l'unità più grande a cui segue sempre l'unità inferiore. Questo tipo di scrittura è noto anche come "scrittura decrescente".
| Rappresentazione conforme all'ISO 8601 | Valori |
|---|---|
| Anno (Y) | YYYY, di quattro cifre, abbreviato in due |
| Mese (M) | MM, da 01 a 12 |
| Settimana (W) | WW, da 01 a 53 |
| Giorno (D) | D, giorno della settimana, da 1 a 7 |
| Ora (h) | hh, da 00 a 23, 24:00:00 come orario finale |
| Minuti (m) | mm, da 01 a 59 |
| Secondi (s) | ss, da 01 a 59 |
| Frazioni decimali (f) | Frazioni di secondo, precisioni facoltative |
La data è l'ora nella stringa ISO, sono divise dalla lettera "T", ad esempio:
25 luglio 1980 ore 15:30:10 = "1980-07-25'T'15:30:10".
Dopo l'indicazione della data e dell'orario, spesso si esprime anche la differenza rispetto al tempo universale coordinato, abbreviato con la sigla UTC. In questo modo il formato tiene conto anche degli eventuali diversi fusi orari o dell'ora legale specifica di un paese.
Ad esempio, la stinga ISO seguente:
2020-11-16T04:25:03-05:00
indica la data e l'ora solare di una località ad Ovest di Greenwich (meridiano 0), perché c'è il segno meno, cinque ore prima dell'ora UTC; Il segno -/+ indica il numero di ore prima (Ovest) o dopo (Est) dell'ora UTC.
2020-11-16T04:25:03Z
Il calendario gregoriano è il calendario solare ufficiale adottato da quasi tutti i paesi del mondo. Fu introdotto da papa Gregorio XIII nel 1582 come correzione del precedente calendario giuliano (di epoca romana), il quale era sfasato di 11 minuti ogni anno solare.
Il calendario giuliano aggiunge un giorno al calendario ogni 4 anni. Il calendario gregoriano fa lo stesso, tranne quando l'anno è divisibile per 100 e non divisibile per 400.
Clicca qui per vedere come facciamo in programmazione a capire se un anno è secolare e bisestile.
Esempio 9
Visualizzare la data e l'ora corrente e le informazioni del Time zone sia in formato standard, sia in formato ISO 8601.
Soluzione Python:
# Gestione date e ore in formato ISO
import datetime as dt
dataObj=dt.datetime.now()
print("Data e ora: "+str(dataObj))
print("ISO 8601: "+dataObj.isoformat())
Soluzione JavaScript (node.js):
const dataObj = new Date();
console.log("Data e ora: " + dataObj.toString());
console.log("ISO 8601: " + dataObj.toISOString());
Esempio 10
Trasformare la data e l'ora corrente e le informazioni del Time zone da formato standard in formato ISO 8601.
Soluzione Python:
# Gestione date e ore in formato ISO
import datetime as dt
dataObj = dt.datetime.now()
print(dataObj.strftime('%Y-%m-%dT%H:%M:%S.%f%z'))
// Ottieni la data attuale
const dataObj = moment();
// Formatta la data nel formato ISO richiesto
console.log(dataObj.format('YYYY-MM-DDTHH:mm:ss.SSSZ'));
Esempio 11
Stampare in formato ISO 8601, le informazioni del Time zone UTC.
Sempre in formato ISO 8601, stampare anche le informazioni del Time zone Europe/Rome.
Infine, stampare la differenza di fuso orario tra l'ora locale di Roma e l'UTC.
Soluzione Python:
# Gestione date ISO
import datetime as dt
import pytz
dataObj = dt.datetime.now()
dataObjUTC=dataObj.astimezone(pytz.timezone("UTC"))
dataObjRM=dataObj.astimezone(pytz.timezone("Europe/Rome"))
print("Informazioni Time zone UTC: "+dataObjUTC.strftime('%Y-%m-%dT%H:%M:%S.%f%z'))
print("Informazioni Time zone Roma: "+str(dataObjRM.strftime('%Y-%m-%dT%H:%M:%S.%f%z')))
print("Offset tra fuso orario UTC e Roma: "+str(dataObjRM.utcoffset()))
// Ottieni la data attuale
const dataObj = moment();
// Converti in UTC
const dataObjUTC = dataObj.tz('UTC');
console.log("Informazioni Time zone UTC: " + dataObjUTC.format('YYYY-MM-DDTHH:mm:ss.SSSZ'));
// Converti in fuso orario di Roma
const dataObjRM = dataObj.tz('Europe/Rome');
console.log("Informazioni Time zone Roma: " + dataObjRM.format('YYYY-MM-DDTHH:mm:ss.SSSZ'));
// Offset tra UTC e Roma
const offset = dataObjRM.utcOffset() / 60; // Ottieni l'offset in ore
console.log("Offset tra fuso orario UTC e Roma: " + offset + " ore");
Prima di eseguire il programma assicurati di aver installato il modulo moment-timezone.
Leggi anche le altre lezioni ...
COMPETENZE PER PROGRAMMARE:
1-I sistemi di numerazione
2-Mondo reale e Mondo Digitale
3-La reppresentazione digitale dei numeri interi e decimali
4-Le stringhe
5-Le espressioni regolari (REGEXP)
Segui sul canale YouTube "Skill Factory Channel" la Playlist: COMPETENZE PER PROGRAMMARE
TUTORIALS
1-Laboratori di logica di programmazione in C
2-Impariamo a programmare con JavaScript
3-Ricominciamo dal linguaggio SQL
4-Introduzione alla logica degli oggetti
5-TypeScript
6-Impariamo a programmare in Python
7-Come sviluppare un sito in WordPress
PAR GOL (Garanzia di Occupabilità dei Lavoratori)

Se sei residente in Campania e cerchi lavoro, sai che puoi partecipare gratuitamente ad un corso di formazione professionale PAR GOL?
I corsi di formazione professionale PAR GOL sono finanziati dalla Regione Campania e ti permettono di acquisire una Qualifica Professionale Europea (EQF) e di partecipare ad un tirocinio formativo aziendale.
Invia il tuo CV o una manifestazione d'interesse a: recruiting@skillfactory.it
oppure
chiama ai seguenti numeri di telefono:
Tel.: 081/18181361
Cell.: 327 0870141
oppure
Contattaci attraverso il nostro sito: www.skillfactory.it
Per maggiori informazioni sul progetto PAR GOL, clicca qui.
Per maggiori informazioni sulle Qualifiche Professionali Europee (EQF), clicca qui.
Academy delle professioni digitali
Per consultare il catalogo dei corsi online della nostra Academy ...

... collegati al nostro sito: www.skillfactory.it
Come progettare e sviluppare giochi per l'educazione e la formazione con Python: lezione 4
![]() Mirko Onorato |
Mirko Onorato |
 Skill Factory - 15/07/2024 23:52:03 | in Tutorials
Skill Factory - 15/07/2024 23:52:03 | in Tutorials
In questa lezione finalmente implementeremo la prima esperienza in HAMMER-XP, l'obiettivo sarà quello di eliminare tutti i numeri pari tra 1 e 100.

L'idea è quella di visualizzare nell'area di gioco una tabella con 100 sprite rettangolari di colore blue che contengono i numeri da 1 a 100. Se Hammer tocca uno sprite che contiene un numero pari lo score s'incrementa di uno, se per sbaglio si tocca un sprite che contiene un numero dispari allora sarà il wrong a incrementarsi di uno.
Il gioco s'interromperà con il messaggio GAME OVER se il numero di wrong (errori) supererà il numero di score (successi) oppure se il tempo di gioco supererà i 120 secondi (2 minuti).
Il gioco terminerà con il messaggio GOOL!!!, se verranno eliminati tutti i numeri pari nel tempo utile.
LA CLASSE BLOCCO
La classe seguente servirà per creare gli oggetti sprite che conterranno i numeri da 1 a 100. Una classe è un modello per creare oggetti da utilizzare nei programmi.
Una classe può ereditare il codice di altre classi per specializzarsi a fare qualcosa. La classe Blocco ereditando la classe pygame.sprite.Sprite si specializza nella gestione di sprite perché eredità tutti gli attributi e i metodi che serviranno all'oggetto creato per comportarsi come un sprite.
# Questa classe permette di creare gli oggetti sprite rettangolari con i numeri
class Blocco(pygame.sprite.Sprite):
# Costruttore dello sprite
def __init__(self, color, width, height, text, hit):
super().__init__()
self.hit=hit
self.numero=int(text)
self.image = pygame.Surface([width, height])
self.rect = self.image.get_rect()
self.font= pygame.font.SysFont('arialunicode', 30)
self.textSurf = self.font.render(text, 1, (255,255,255))
self.image = pygame.Surface((width, height))
W = self.textSurf.get_width()
H = self.textSurf.get_height()
self.image.fill(color)
# Centra il testo nel blocco sprite
self.image.blit(self.textSurf, [width/2 - W/2, height/2 - H/2])
Il costruttore __init__ è il metodo di una classe usato per inizializzare l'oggetto creato, gli argomenti del costruttore:
def __init__(self, color, width, height, text, hit),
sono importanti per capire quali informazioni si dovranno passare alla classe per creare un oggetto di quel tipo. In questo caso per creare uno sprite di tipo Blocco sono richieste le seguenti informazioni:
color=colore dello sprite in formato (red, green, blue)
width=larghezza in pixel dello sprite
height=altezza in pixel dello sprite
text=testo che corrisponderà al numero visualizzato nello sprite
hit=questo parametro potrà contenere False oppure True (False se il numero assegnato allo sprite sarà dispari, True se il numero assegnato allo sprite sarà pari).
Il comando self.rect = self.image.get_rect() è importante perché permette di creare l'oggetto serf.rect con gli attributi x e y, corrispondenti alle coordinate della posizione di uno sprite sullo schermo.
Assegnando un valore a self.rect.x e self.rect.y sarà possibile posizionare qualunque sprite creato all'interno dello schermo.
Vediamo un esempio:
BLUE=(0,0,255) # RED=0 GREEN=0 BLUE=255, impostiamo il colore BLUE con la codifica RGB
primoBloccoSprite=Blocco(BLUE, 35, 35,"1",False)
il codice Python precedente crea un oggetto sprite di nome primoBloccoSprite di colore blue e di 35X35 pixel. Al centro dello sprite verrà visualizzato il numero 1, quindi il parametro hit dovrà essere impostato a False, perché il numero è dispari.
secondoBloccoSprite=Blocco(BLUE, 35, 35,"2",True)
il codice Python precedente crea un oggetto sprite di nome secondoBloccoSprite di colore blue e di 35X35 pixel. Al centro dello sprite verrà visualizzato il numero 2, quindi il parametro hit dovrà essere impostato a True, perché il numero è pari.
I comandi seguenti:
primoBloccoSprite.rect.x=100
primoBloccoSprite.rect.y=50
secondoBloccoSprite.rect.x=140
secondoBloccoSprite.rect.y=50
permettono di posizionare i due sprite nell'area di gioco, il primo alla posizione di coordinate (100, 50), il secondo alla posizione di coordinate (140, 50).

COME CREARE E DISPORRE NELL'AREA DI GIOCO GLI SPRITE CON I NUMERI DA 1 A 100
Il codice Python seguente mostra come creare e disporre sull'area di gioco gli sprite con i numeri da 1 a 100:
BLUE=(0, 0, 255) # impostiamo il colore blue
pos_x=55
pos_y=2
for x in range(1,101): # range genera un vettore di numeri interi da 1 a 100, per ogni numero del vettore il for esegue i comandi associati
if x%2==0:
hit=True # Se il numero è pari imposta hit=True
else:
hit=False # Se il numero è dispari imposta hit=False
blocco = Blocco(BLUE, 35, 35,str(x),hit) # Crea un blocco di tipo sprite che visualizzera il valore del numero x corrente
# Posiziona gli sprite creati nell'area di gioco
blocco.rect.x=pos_x
pos_x+=44
blocco.rect.y=pos_y
# Aggiunge gli sprite creati ai gruppi di sprite
block_list.add(blocco)
sprite_list.add(blocco)
# Cambia riga dell'area di gioco quando gli sprite hanno occupato tutto lo spazio disponibile sulla riga corrente
if x==25 or x==50 or x==75:
pos_x=50
pos_y+=108


def __init__(self):
super(Hammer, self).__init__()
# Carica l'immagine di Hammer
self.image=pygame.image.load('hammer.png')
# Imposta le dimensioni dell'immagine larghezza, altezza
self.image = pygame.transform.scale(self.image, (25,50))
self.images = []
self.images.append(self.image) # Associamo allo sprite l'immagine di Hammer
self.index = 0
self.x=0
self.y=0
self.image = self.images[self.index]
self.rect = self.image.get_rect()
if not gameOver:
# pos è una tupla che coterrà le coordinate x,y del puntatore del mouse
pos = pygame.mouse.get_pos()
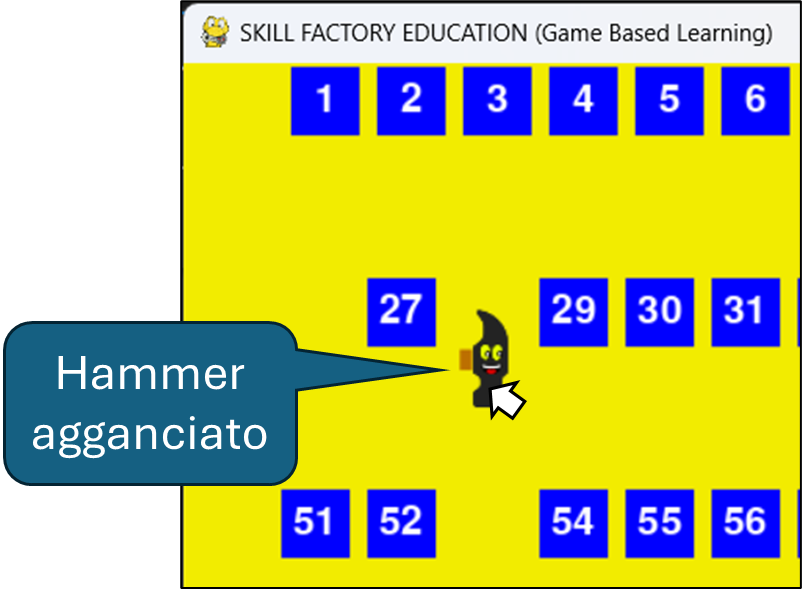
if pos[0]>=pos_hammer[0] and pos[0]<=pos_hammer[1] and pos[1]>=pos_hammer[2] and pos[1]<=pos_hammer[3]:
hammer_agganciato=True
if hammer_agganciato:
# I controlli seguenti limitano i movimenti di HAMMER solo nella sezione di gioco
if pos[0]>5 and pos[0]<1180 and pos[1]>25 and pos[1]<344:
hammer.rect.x=pos[0]-5
hammer.rect.y=pos[1]-25
else:
hammer_agganciato=False
if pos[1]<=25:
hammer.rect.y=0
elif pos[1]>=344:
hammer.rect.y=319
if pos[0]<=5:
hammer.rect.x=0
elif pos[0]>=1175:
hammer.rect.x=1175
pos_hammer[0]=hammer.rect.x
pos_hammer[1]=hammer.rect.x+25
pos_hammer[2]=hammer.rect.y
pos_hammer[3]=hammer.rect.y+50

pos_y=430
for testo in scheda:
riga = font.render(testo, True, (255,255,255))
screen.blit(riga, (20, pos_y))
pos_y+=27
def show_info(screen, informazioni_del_gioco,wrong_value,score_value,s_tempo,age_value,scheda):
font= pygame.font.SysFont('Verdana', 20)
pos_y=430
for testo in scheda:
riga = font.render(testo, True, (255,255,255))
screen.blit(riga, (20, pos_y))
pos_y+=27
font= pygame.font.SysFont('arialunicode', 30)
exp = font.render(str(informazioni_del_gioco.experience_value), True, (255,255,255))
screen.blit(exp, (820, 430))
level = font.render(str(informazioni_del_gioco.level_value), True, (255,255,255))
screen.blit(level, (1100, 430))
wrong = font.render(str(wrong_value), True, (255,255,255))
screen.blit(wrong, (820, 510))
score = font.render(str(score_value), True, (255,255,255))
screen.blit(score, (1100, 510))
t = font.render(s_tempo, True, (255,255,255))
screen.blit(t, (715, 585))
age = font.render(str(age_value), True, (255,255,255))
screen.blit(age, (1100, 585))
La funzione struttura_tempo riceve il tempo trascorso in secondi e lo converte in una stringa nel formato hh:mm:ss.
Per calcolare il tempo trascorso basta leggere l'ora di sistema quando parte il gioco e confrontarla ogni volta con l'ora di sistema corrente.
Per fare questa operazioni, quando parte il gioco, possiamo usare il comando:
t1=time.time()
La funzione time() dell'oggetto time, legge l'ora di sistema alla partenza del gioco e la converte in secondi trascorsi dal 01/01/1970; salvando questo valore nella variabile t1, conosciamo il numero di secondi trascorsi dal 01/01/1970 all'avvio del gioco.
t2=time.time()
In questo caso la variabile t2 conterrà il numero di secondi trascorsi dal 01/01/1970 all'ora corrente; quindi, per ottenere il numero di secondi trascorsi dall'inizio del gioco basterà calcolare la differenza tra t2 e t1:
def struttura_tempo(t_value):
ore=math.floor(t_value/3600)
minuti=t_value-(ore*3600)
minuti=math.floor(minuti/60)
secondi=t_value-((ore*3600)+(minuti*60))
secondiStr="0"+str(secondi)
minutiStr="0"+str(minuti)
oreStr="0"+str(ore)
s_tempo=oreStr[-2:]+":"+minutiStr[-2:]+":"+secondiStr[-2:]
return s_tempo
LA FUNZIONE CHE CREA IL PRIMO LIVELLO DELLA PRIMA ESPERIENZA DI MATEMATICA
La funzione exp_01_01 viene utilizzata per creare il primo livello della prima esperienza di matematica.
La funzione riceve i seguenti argomenti:
block_list=riferimento del gruppo in cui aggiungere i blocchi dell'esperienza, serve per rilevare le collisioni con Hammer
sprite_list=riferimento del gruppo in cui aggiungere i blocchi dell'esperienza, serve per visualizzare tutti gli sprite creati nell'area di gioco
informazioni_del_gioco=gli attributi di questo oggetto servono per impostare il progressivo dell'esperienza, il livello, lo score obiettivo, la durata del gioco
La classe con cui viene creato questo oggetto è la seguente:
class Informazioni_del_gioco():
# Costruttore dello sprite, quando viene eseguito dovete passare il colore dello sprite, la larghezza e l'altezza in pixel
def __init__(self, experience_value,level_value,score_value_exit,t_value_exit):
super().__init__()
self.experience_value=experience_value
self.level_value=level_value
self.score_value_exit=score_value_exit
self.t_value_exit=t_value_exit
Infine, c'è l'argomento:
scheda=vettore che conterrà le stringhe che corrispondono alle righe che descrivono l'esperienza che si sta giocando
Di seguito il codice completo della funzione exp_01_01:
def exp_01_01(block_list,sprite_list,informazioni_del_gioco,scheda):
BLUE=(0, 0, 255) # impostiamo il colore blue
pos_x=55
pos_y=2
for x in range(1,101):
if x%2==0:
hit=True
else:
hit=False
blocco = Blocco(BLUE, 35, 35,str(x),hit)
# Posiziona gli sprite creati nell'area di gioco
blocco.rect.x=pos_x
pos_x+=44
blocco.rect.y=pos_y
# Aggiunge gli sprite creati ai gruppi di sprite
block_list.add(blocco)
sprite_list.add(blocco)
if x==25 or x==50 or x==75:
pos_x=50
pos_y+=108
informazioni_del_gioco.experience_value=1
informazioni_del_gioco.level_value=1
informazioni_del_gioco.score_value_exit=50 # Il valore di score obiettivo è quello di 50 successi
informazioni_del_gioco.t_value_exit=120 # L'esperienza dura 2 minuti
# Aggiungiamo al vettore scheda le stringhe che corrispondono alle righe che descrivono l'esperienza che si sta giocando
scheda.append("MATEMATICA I")
scheda.append("Elimina dall'area di gioco i numeri pari.")
scheda.append("Il gioco termina se gli errori superano le risposte esatte.")
scheda.append("L'esperienza avrà una durata di 2 minuti.")
scheda.append("Aggancia Hammer con il puntatore del mouse e inizia a")
scheda.append("giocare.")

LA GESTIONE DEI SUCCESSI (SCORE) O DEGLI ERRORI (WRONG) DOPO LE COLLISIONI
Il metodo spritecollide permette di rilevare la collisione tra uno sprite e gli sprite di un gruppo.
Per rilevare le collisioni tra Hammer e i blocchi con i numeri, dovete passare come argomenti alla funzione spritecollide, sia il riferimento dell'oggetto hammer, sia il riferimento del gruppo che contiene i riferimenti dei blocchi con i numeri presenti nell'area di gioco: block_list.
Il terzo argomento della funzione, se impostato a True, indica che l'oggetto che collide con Hammer, dovrà essere eliminato dal gruppo e non dovrà più essere visibile nell'area di gioco.
Gli oggetti che collidono con Hammer vengono aggiunti al gruppo blocks_hit_list; quindi, con un ciclo for possiamo ottenere il riferimento di tutti gli sprite che hanno avuto una collisione con Hummer. Leggendo il valore dell'attributo hit dei blocchi presenti nel gruppo blocks_hit_list sarà possibile capire se il blocco era associato a un numero pari (hit=True) o a un numero dispari (hit=false).
In base allo stato dell'attributo hit (True/False) vengono aggiornati i valori dei contatori wrong e score, come mostra il codice Python seguente:
# Aggiunge al gruppo blocks_hit_list i riferimenti dei blocchi che collidono con l'oggetto hummer
blocks_hit_list = pygame.sprite.spritecollide(hammer, block_list, True)
# Legge il riferimento dei blocchi che hanno avuto una collisione con Hammer e verifica se incrementare il contatore score o wrong
for blocco in blocks_hit_list:
# Genera un suono, come un click, per indicare che c'è stata una collisione
winsound.Beep(3000,1)
# Incrementa di 1 score_value se hit è True (numero pari), altrimenti incrementa di 1 wrong_value se hit è False (numero dispari)
if blocco.hit:
score_value+=1
else:
wrong_value+=1
La funzione Beep della libreria winsound emette un breve suono di 3000 HZ, serve per indicare che Hammer ha toccato un blocco con un numero.
LA FINE DEL GIOCO
Il gioco termina con GAME OVER se il numero di WRONG (Errori) sumera il numero di SCORE (Successi) oppure se il tempo di gioco supera la durata prevista. In questo caso verrà emesso un suono che indica un insuccesso e verrà visualizzata l'etichetta GAME OVER:
 I
I
Il gioco termina con GOAL!!! se viene raggiunto l'obiettivo previsto dall'esperienza che prevede che Hammer elimini dall'area di gioco tutti i blocchi con numeri pari. In questo caso verrà emesso un suono che indica successo e verrà visualizzata l'etichetta GOAL!!!:
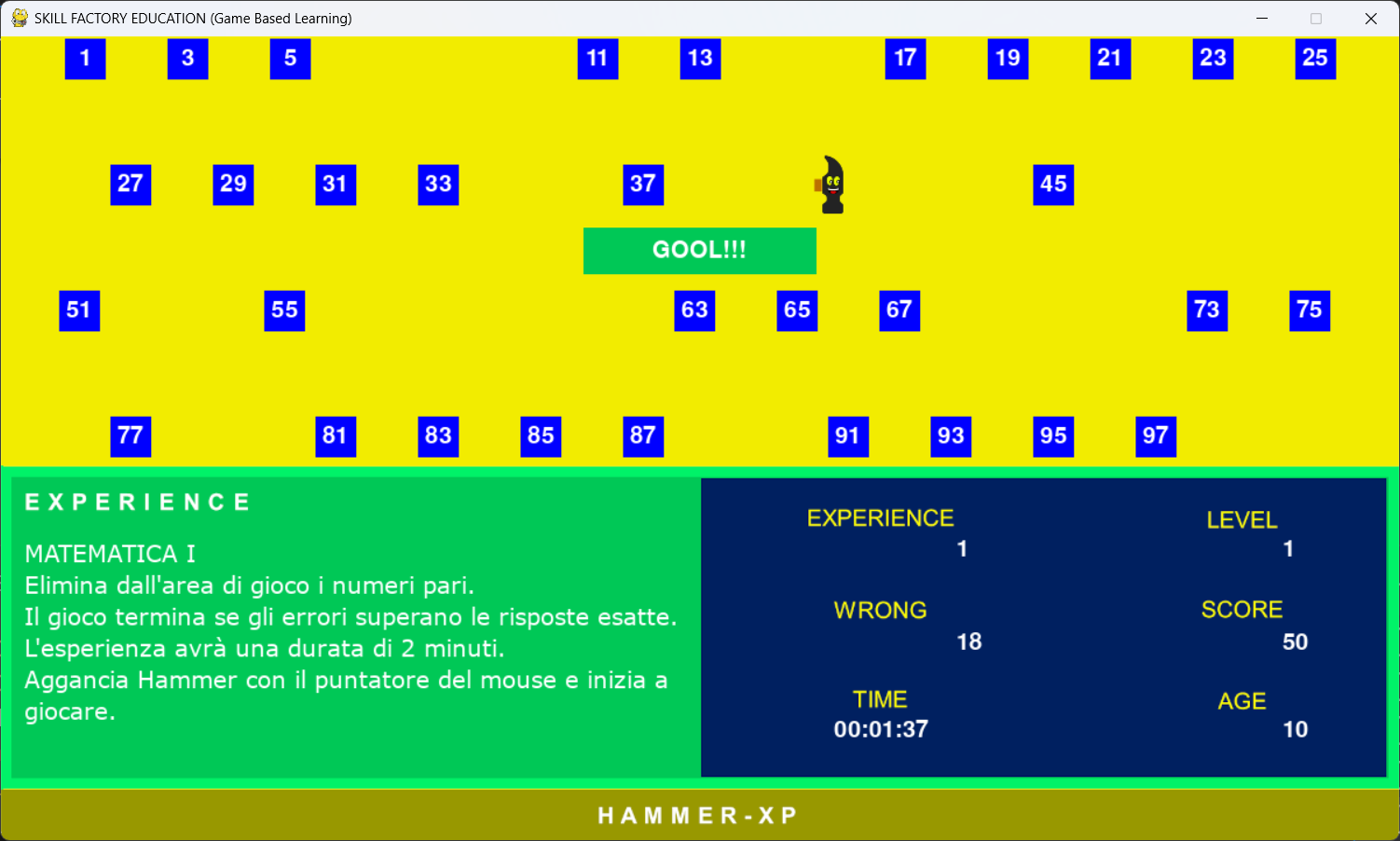
Le etichette GAME OVER e GOAL!!! sono due oggetti sprite creati nel modo seguente:
bloccoGameOver=Etichetta((255,0,0),200,40,500,164,'GAME OVER')
bloccoGoal=Etichetta((0,200,86),200,40,500,164,'GOOL!!!')
Entrambi gli oggetti sono dello stesso tipo, perché sono stati creati con la classe Etichette:
class Etichetta(pygame.sprite.Sprite):
# Quando si crea l'oggeto sprite passare il colore, la larghezza, l'altezza
# la posizione dello sprite nell'ambiente di gioco
def __init__(self, color, width, height, x,y,text):
super().__init__()
self.image = pygame.Surface([width, height])
self.rect = self.image.get_rect()
self.rect.x=x
self.rect.y=y
self.font= pygame.font.SysFont('arialunicode', 30)
self.textSurf = self.font.render(text, 1, (255,255,255))
self.image = pygame.Surface((width, height))
W = self.textSurf.get_width()
H = self.textSurf.get_height()
self.image.fill(color)
self.image.blit(self.textSurf, [width/2 - W/2, height/2 - H/2])
Il codice Python seguente mostra come viene gestita la fine del gioco:
# Il gioco termina se gli errori sono maggiori dei successi, se si va oltre il tempo massimo disponibile, se si raggiunge l'obiettivo previsto
if wrong_value>score_value or t_value==informazioni_del_gioco.t_value_exit or score_value==informazioni_del_gioco.score_value_exit:
# Impostando a True questa variabile vengono inibiti tutti i movimenti di Hummer e la gestione degli eventi, quindi il gioco termina
gameOver=True
# Obiettivo raggiunto
if score_value==informazioni_del_gioco.score_value_exit:
sprite_list.add(bloccoGoal)
beep_goal()
else: # Obiettivo non raggiunto
beep_game_over()
sprite_list.add(bloccoGameOver)
Per gestire le tonalità sonore che indicano il successo oppure l'insuccesso sono state create le funzioni:
beep_goal() # Successo
beep_game_over() # Insuccesso
def beep_goal():
frequenza=150
durata=[400,150,200,250,700]
for x in range(5):
winsound.Beep(frequenza,durata[x])
frequenza+=150
winsound.Beep(frequenza,1000)
# Genera una tonalità che indica un insuccesso
def beep_game_over():
frequenza=400
durata=[600,300,200,300,700]
for x in range(5):
winsound.Beep(frequenza,durata[x])
frequenza-=30
winsound.Beep(frequenza,1000)
COME ESEGUIRE IL GIOCO
Per eseguire il gioco HAMMER-XP dovete installare il framework Python sul vostro computer.
Per eseguire il download del setup per installare Python clicate qui oppure collegatevi al link seguente: https://www.python.org/downloads/.
Dopo il download del setup, eseguitelo per installare Python.
Attenzione, durante l'installazione è importante spuntare l'opzione "Add Python 3.X to PATH:

Dopo che avete impostato l'opzione, cliccate sul comando Install Now.
Per verificare se il framework Python è stato installato correttamente, dal prompt dei comandi del sistema operativo, eseguite il comando:
python --version
Se l'installazione è andata a buon fine viene visualizzata la versione di Python, come mostra l'immagine seguente:

Successivamente create una cartella "HAMMER-XP", in questa cartella copiate i file seguenti:
hammer_experience_matematica_001_V01.py
hammer.png
sfondo_hammer_xp.png
Per il download dello zip con i tre file cliccate qui.
Estraete i file nella cartella "HAMMER-XP".
Per avviare il gioco fate doppio click sul file hammer_experience_matematica_001_V01.py.
Nella prossima lezione aggiungeremo all'esperienza di Matematica I, altri 3 livelli:
1) Elimina 3 e i multipli di 3;
2) Elimina 7 e i divisori di 7;
3) Elimina i numeri primi.
< LEZIONE PRECEDENTE | LEZIONE SUCCESSIVA > | VAI ALLA PRIMA LEZIONE
T U T O R I A L S S U G G E R I T I
- Competenze per programmare
- Impariamo Python giocando al "Solitario del ferroviere"
- Impariamo a programmare con JavaScript
- Laboratori di Logica di programmazione in C
- Introduzione alla Logica degli oggetti
- Ricominciamo ... dal Linguaggio SQL
- APP Mania
- Come sviluppare un Sito con Wordpress
PER IMPARARE A PROGRAMMARE, SEGUI LE PLAYLIST SUL NOSTRO CANALE YOUTUBE "SKILL FACTORY CHANNEL": clicca qui per accedere alle playlist
PAR GOL (Garanzia di Occupabilità dei Lavoratori)

Se sei residente in Campania e cerchi lavoro, sai che puoi partecipare gratuitamente ad un corso di formazione professionale PAR GOL?
I corsi di formazione professionale PAR GOL sono finanziati dalla Regione Campania e ti permettono di acquisire una Qualifica Professionale Europea (EQF) e di partecipare ad un tirocinio formativo aziendale.
Invia il tuo CV o una manifestazione d'interesse a: recruiting@skillfactory.it
oppure
chiama ai seguenti numeri di telefono:
Tel.: 081/18181361
Cell.: 327 0870141
oppure
Contattaci attraverso il nostro sito: www.skillfactory.it
Per maggiori informazioni sul progetto PAR GOL, clicca qui.
Per maggiori informazioni sulle Qualifiche Professionali Europee (EQF), clicca qui.
Academy delle professioni digitali
Per consultare il catalogo dei corsi online della nostra Academy ...

... collegati al nostro sito: www.skillfactory.it
Come progettare e sviluppare giochi per l'educazione e la formazione con Python: lezione 3
![]() Mirko Onorato |
Mirko Onorato |
 Skill Factory - 27/06/2024 10:07:44 | in Tutorials
Skill Factory - 27/06/2024 10:07:44 | in Tutorials
In questa nuova lezione imparerete a muovere Hammer nell'area di gioco, utilizzando il puntatore del mouse e a gestire le collisioni con altri sprite.
Prima di tutto dobbiamo definire le coordinate dell'area di gioco in cui sia Hammer, sia gli altri sprite potranno muoversi.
L'immagine seguente mostra le dimensioni dell'interfaccia espresse in pixel.
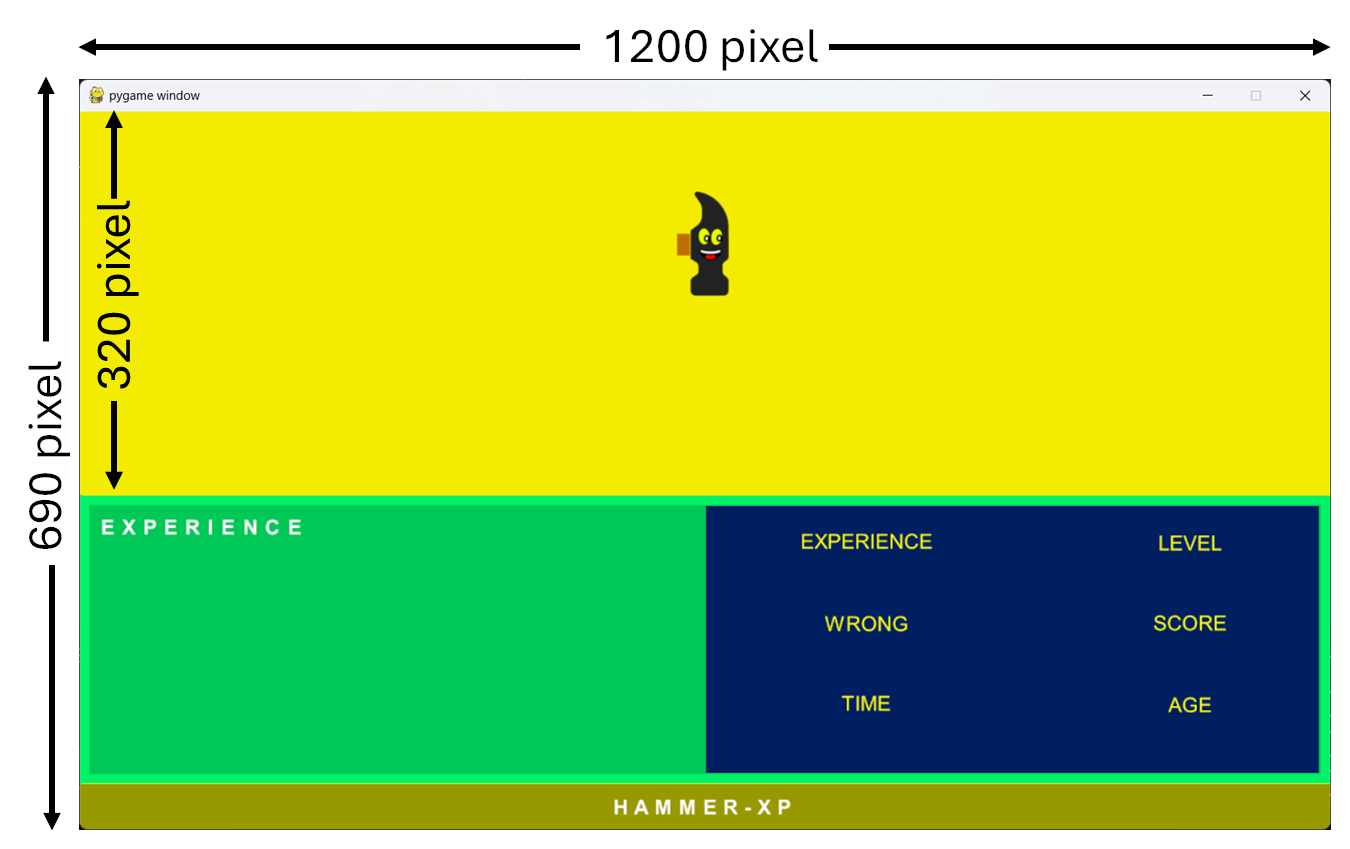
L'interfaccia del gioco ha una larghezza di 1200 pixel e un'altezza di 690 pixel, mentre l'area di gioco ha una larghezza di 1200 pixel e un'altezza di 320 pixel.
COME MUOVERE HAMMER USANDO IL PUNTATORE DEL MOUSE
Per associare i movimenti di Hammer al puntatore del mouse, servono le coordinate x, y del puntatore.
Il comando seguente cattura le coordinate x, y delle posizioni del mouse nella finestra di gioco:
pos = pygame.mouse.get_pos()
La variabile pos è una tupla, quindi:
pos[0] indica la coordinata x del mouse, nella posizione corrente, mentre
pos[1] indica la coordinata y del mouse, nella posizione corrente.
Per associare il movimento dal mouse ad Hammer, dovete usare il codice seguente:
hammer.rect.x=pos[0]-5
hammer.rect.y=pos[1]-50
Alla posizione x del mouse sottraiamo 5 pixel e a quella y sottraiamo 50 pixel, per posizionare il puntatore del mouse sul manico del martelletto, come mostra la figura seguente:
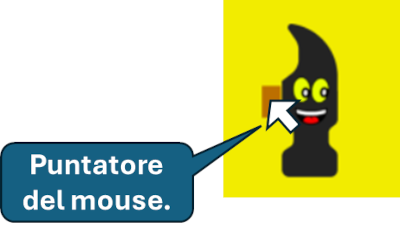
COME LIMITARE I MOVIMENTI DI HAMMER ALL'AREA DI GIOCO
Per evitare che Hammer si sposti oltre l'area di gioco, dovete verificare che le coordinate pos[0] e pos[1] non assumano valori esterni al perimetro dell'area di gioco. Quando si verifica questa condizione i valori di pos[0] e pos[1] vanno impostati in modo che Hammer non superi i limiti definiti dal perimetro di gioco.
Il codice Python seguente vi permetterà di limitare i movimenti di Hammer, solo all'interno dell'area di gioco:
# Legge la coordinate della posizione del puntatore del mouse
pos = pygame.mouse.get_pos()
# Se le coordinte pos[0] e pos[1] si trovano nel perimetro dell'area di gioco Hammer si sposta insieme al puntatore del mouse
if pos[0]>0 and pos[0]<1156 and pos[1]>50 and pos[1]<320:
hammer.rect.x=pos[0]-5
hammer.rect.y=pos[1]-50
# Se le coordinte pos[0] e pos[1] si trovano fuori dal perimetro dell'area di gioco Hammer si ferma
else:
if pos[1]<=50:
hammer.rect.y=0
elif pos[1]>=320:
hammer.rect.y=268
if pos[0]<=0:
hammer.rect.x=0
elif pos[0]>=1156:
hammer.rect.x=1150
Di seguito trovate il codice Python completo per muovere Hammer all'interno dell'area di gioco:
import pygame
SIZE = WIDTH, HEIGHT = 1200, 690 # Impostiamo la larghezza e l'altezza dello schermo
# Carichiamo l'immagine di sfondo del gioco
SFONDO = pygame.image.load("sfondo_hammer_xp.png")
# La classe seguente permette di creare lo sprite e le sue caratteristiche
class Hammer(pygame.sprite.Sprite):
def __init__(self):
super(Hammer, self).__init__()
self.images = []
self.images.append(pygame.image.load('hammer.png')) # Associamo allo sprite l'immagine di hammer
self.index = 0
self.x=0
self.y=0
self.image = self.images[self.index]
self.rect = self.image.get_rect()
def main():
# Inizializziamo l'ambiente pygame
pygame.init()
# Impostiamo le dimensioni dello schermo
screen = pygame.display.set_mode(SIZE)
# Creiamo lo sprite hammer usando la classe sprite Hammer
hammer = Hammer()
# Creiamo il gruppo che contiene gli sprite del gioco
sprite_group = pygame.sprite.Group()
# Aggiungiamo al gruppo lo sprite hammer
sprite_group.add(hammer)
# Gestiamo gli eventi prodotti dal giocatore
while True:
for event in pygame.event.get():
# Interrompiamo il gioco se clicchiamo sulla X di fine gioco
if event.type == pygame.QUIT:
pygame.quit()
quit()
# Impostiamo la posizione di HAMMER attraverso il movimento del mouse
pos = pygame.mouse.get_pos()
# I controlli seguenti limitano i movimenti di HAMMER solo nella sezione di gioco
if pos[0]>0 and pos[0]<1156 and pos[1]>50 and pos[1]<320:
hammer.rect.x=pos[0]-5
hammer.rect.y=pos[1]-50
else:
if pos[1]<=50:
hammer.rect.y=0
elif pos[1]>=320:
hammer.rect.y=268
if pos[0]<=0:
hammer.rect.x=0
elif pos[0]>=1156:
hammer.rect.x=1150
# Disegniamo l'immagine come sfondo del gioco
screen.blit(SFONDO,(0,0))
# Disegniamo tutti gli sprite associati al gruppo sullo schermo
sprite_group.draw(screen)
# Aggiorniamo lo schermo per vedere i cambiamenti
pygame.display.update()
# Avvia il programma eseguendo il metodo main()
if __name__ == '__main__':
main()
COME AGGIUNGERE ALTRI SPRITE ALL'AREA DI GIOCO DI HAMMER-XP
Per creare le esperienze di gioco occorre aggiungere all'area di gioco di HAMMER-XP altri sprite.
Come avete già visto nella lezione precedente per creare uno sprite serve prima la classe seguente, che ne rappresenta il tipo:
class MioSprite(pygame.sprite.Sprite):
# Costruttore dello sprite, quando viene eseguito dovete passare il colore dello sprite, la larghezza e l'altezza in pixel
def __init__(self, color, width, height):
super().__init__()
self.image = pygame.Surface([width, height])
self.image.fill(color)
self.rect = self.image.get_rect()
Definito il tipo (classe), per creare un oggetto sprite da aggiungere al gioco, dovete usare il codice Python seguente:
RED=(255, 0, 0) # impostiamo il colore rosso
primoSprite = MioSprite(RED, 30, 30)
In questo caso abbiamo creato uno sprite che corrisponde ad un blocco di colore rosso di 30X30 pixel.
Adesso impostiamo la posizione dello sprite creato nell'area di gioco:
primoSprite.rect.x=500
primoSprite.rect.y=145
Con il codice Python seguente creiamo un nuovo sprite, ma di colre blu:
BLUE=(0, 0, 255) # impostiamo il colore blu
secondoSprite = MioSprite(BLUE, 30, 30)
Adesso impostiamo la posizione dello sprite creato nell'area di gioco:
secondoSprite.rect.x=670
secondoSprite.rect.y=145
block_list = pygame.sprite.Group()
Successivamente dovete aggiungere al gruppo gli sprite creati:
block_list.add(primoSprite)
block_list.add(secondoSprite)
infine per completare l'operazione dovete usare i comandi segueti:
sprite_group.draw(screen)
pygame.display.update()
Di seguito trovate il codice Python completo per disegnare i due sprite dell'area di gioco:
import pygame
SIZE = WIDTH, HEIGHT = 1200, 690 # Impostiamo la larghezza e l'altezza dello schermo
# Carichiamo l'immagine di sfondo del gioco
SFONDO = pygame.image.load("sfondo_hammer_xp.png")
# Impostiamo una classe che serve a creare sprite
class MioSprite(pygame.sprite.Sprite):
# Costruttore dello sprite, quando viene eseguito dovete passare il colore dello sprite, la larghezza e l'altezza in pixel
def __init__(self, color, width, height):
super().__init__()
self.image = pygame.Surface([width, height])
self.image.fill(color)
self.rect = self.image.get_rect()
def main():
# Inizializziamo l'ambiente pygame
pygame.init()
# Impostiamo le dimensioni dello schermo
screen = pygame.display.set_mode(SIZE)
# Creaiamo un primo sprite di colore rosso 30X30
RED=(255, 0, 0) # impostiamo il colore rosso
primoSprite = MioSprite(RED, 30, 30)
# Posizioniamo lo sprite creato alle coordinate x=500 e y=145 dell'area di gioco
primoSprite.rect.x=500
primoSprite.rect.y=145
# Creaiamo un secondo sprite di colore rosso 30X30
BLUE=(0, 0, 255) # impostiamo il colore blu
secondoSprite = MioSprite(BLUE, 30, 30)
# Posizioniamo lo sprite creato alle coordinate x=500 e y=145 dell'area di gioco
secondoSprite.rect.x=670
secondoSprite.rect.y=145
# Creaiamo un gruppo di sprite
block_list = pygame.sprite.Group()
# Aggiungiamo al gruppo gli sprite creati
block_list.add(primoSprite)
block_list.add(secondoSprite)
# Gestiamo gli eventi prodotti dal giocatore
while True:
for event in pygame.event.get():
# Interrompiamo il gioco se clicchiamo sulla X di fine gioco
if event.type == pygame.QUIT:
pygame.quit()
quit()
# Disegniamo l'immagine come sfondo del gioco
screen.blit(SFONDO,(0,0))
# Disegniamo tutti gli sprite associati al gruppo sullo schermo
block_list.draw(screen)
# Aggiorniamo lo schermo per vedere i cambiamenti
pygame.display.update()
# Avvia il programma eseguendo il metodo main()
if __name__ == '__main__':
main()
Eseguendo il programma Python otterrete la schermata seguente:
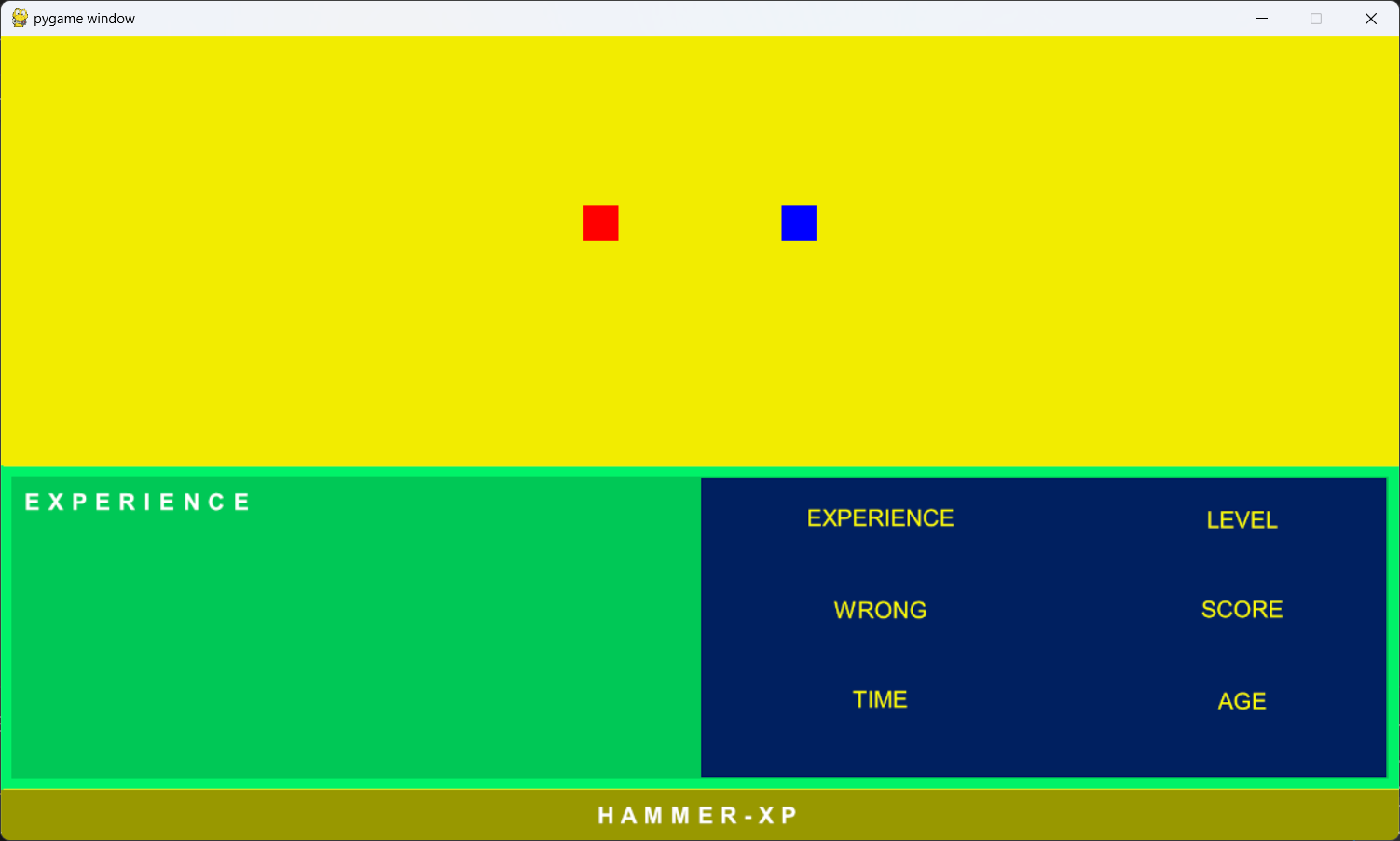
COME AGGIUNGERE ALL'AREA DI GIOCO 10 BLOCCHI COLORATI IN POSIZIONI CASUALI
Per creare 10 blocchi colorati in posizioni casuali prima di tutto dovete importare la libreria random per generare numeri casuali.
Poi serve un vettore che contiene i colori da assegnare agli sprite, come mostra il codice Python seguente:
RED=(255, 0, 0) # impostiamo il colore rosso
GREEN=(0,255,0) # impostiamo il colore verde
BLUE=(0,0,255) # impostiamo il colore blue
colori=[RED,GREEN,BLUE] # impostiamo un vettore con i tre colori
Per ottenere un colore casuale basterà generare un indice casuale tra 0 e 2 come mostra il codice Python seguente:
indice=random.randint(0,2)
colore=colori[indice]
Le posizioni casuali dei blocchi colorati le potete generare con il codice Python seguente:
blocco.rect.x = random.randrange(1170)
blocco.rect.y = random.randrange(339)
Il metodo randrange genera un valore casuale compreso tra 0 e il valore passato come argomento. In questo caso gli argomenti passati rappresentano i limiti massimi della larghezza e dell'altezza dell'area di gioco.
Di seguito trovate il codice Python completo per disegnare 10 sprite colorati in posizioni casuali dell'area di gioco:
import pygame
import random
SIZE = WIDTH, HEIGHT = 1200, 690 # Impostiamo la larghezza e l'altezza dello schermo
# Carichiamo l'immagine di sfondo del gioco
SFONDO = pygame.image.load("sfondo_hammer_xp.png")
RED=(255, 0, 0) # impostiamo il colore rosso
GREEN=(0,255,0) # impostiamo il colore verde
BLUE=(0,0,255) # impostiamo il colore blue
colori=[RED,GREEN,BLUE] # impostiamo un vettore con i tre colori
indice=0
# Impostiamo una classe che serve a creare sprite
class Blocco(pygame.sprite.Sprite):
# Costruttore dello sprite, quando viene eseguito dovete passare il colore dello sprite, la larghezza e l'altezza in pixel
def __init__(self, color, width, height):
super().__init__()
self.image = pygame.Surface([width, height])
self.image.fill(color)
self.rect = self.image.get_rect()
def main():
# Inizializziamo l'ambiente pygame
pygame.init()
# Impostiamo le dimensioni dello schermo
screen = pygame.display.set_mode(SIZE)
# Creaiamo un gruppo di sprite
block_list = pygame.sprite.Group()
for x in range (10):
# Creaiamo un valore casuale che corrisponde a un indice tra 0 e 2
indice=random.randint(0,2)
colore=colori[indice]
blocco = Blocco(colore, 30, 30)
# Impostiamo una posizione casuale per il blocco creato
blocco.rect.x = random.randrange(1170)
blocco.rect.y = random.randrange(339)
# Aggiungiamo al gruppo gli sprite creati
block_list.add(blocco)
# Gestiamo gli eventi prodotti dal giocatore
while True:
for event in pygame.event.get():
# Interrompiamo il gioco se clicchiamo sulla X di fine gioco
if event.type == pygame.QUIT:
pygame.quit()
quit()
# Disegniamo l'immagine come sfondo del gioco
screen.blit(SFONDO,(0,0))
# Disegniamo tutti gli sprite associati al gruppo sullo schermo
block_list.draw(screen)
# Aggiorniamo lo schermo per vedere i cambiamenti
pygame.display.update()
# Avvia il programma eseguendo il metodo main()
if __name__ == '__main__':
main()
Eseguendo il programma Python otterrete la schermata seguente:

COME GESTIRE LE COLLISIONI TRA HAMMER E GLI ALTRI SPRITE DELL'AREA DI GIOCO
Per rilevare le collisioni tra uno sprite e un gruppo di sprite, dovete usare il metodo spritecollide:
blocks_hit_list = pygame.sprite.spritecollide(hammer, block_list, True)
Questo metodo restituisce la lista dei riferimenti degli sprite del gruppo che intersecano lo sprite che non appartiene al gruppo.
Il primo argomento del metodo è il riferimento dello sprite di cui volete rilevare le collisioni; nel nostro caso l'oggetto hammer (sprite).
Il secondo argomento è il riferimento del gruppo che contiene i riferimenti degli sprite con cui lo sprite hammer collide; nel nostro caso i blocchi presenti sull'area di gioco.
L'ultimo argomento è un valore booleano; quando è True il blocco che colliderà con lo sprite hammer verrà eliminato dalla memoria; quindi non potrà più essere visibile perché verrà eliminato anche da tutti i gruppi in cui è stato aggiunto.
Quindi per eliminare dall'area di gioco i blocchi con cui lo sprite hammer colliderà, serviranno due gruppi: il primo gruppo conterrà i riferimenti di tutti gli sprite che dovranno essere visibili nell'area di gioco, incluso lo sprite hammer; invece il secondo gruppo dovrà contenere solo gli sprite di tipo blocco da fornire come argomento al metodo spritecollode.
Il programma Python seguente visualizzerà 10 blocchi colorati in posizioni casuali, i blocchi verranno eliminati dall'area di gioco quando Hammer li interseca:
import pygame
import random
SIZE = WIDTH, HEIGHT = 1200, 690 # Impostiamo la larghezza e l'altezza dello schermo
# Carichiamo l'immagine di sfondo del gioco
SFONDO = pygame.image.load("sfondo_hammer_xp.png")
RED=(255, 0, 0) # impostiamo il colore rosso
GREEN=(0,255,0) # impostiamo il colore verde
BLUE=(0,0,255) # impostiamo il colore blue
colori=[RED,GREEN,BLUE] # impostiamo un vettore con i tre colori
indice=0
# Impostiamo La classe che serve a creare lo sprite Hammer
class Hammer(pygame.sprite.Sprite):
def __init__(self):
super(Hammer, self).__init__()
self.images = []
self.images.append(pygame.image.load('hammer.png')) # Associamo allo sprite l'immagine di hammer
self.index = 0
self.x=0
self.y=0
self.image = self.images[self.index]
self.rect = self.image.get_rect()
# Impostiamo una classe che serve a creare sprite
class Blocco(pygame.sprite.Sprite):
# Costruttore dello sprite, quando viene eseguito dovete passare il colore dello sprite, la larghezza e l'altezza in pixel
def __init__(self, color, width, height):
super().__init__()
self.image = pygame.Surface([width, height])
self.image.fill(color)
self.rect = self.image.get_rect()
def main():
# Inizializziamo l'ambiente pygame
pygame.init()
# Impostiamo le dimensioni dello schermo
screen = pygame.display.set_mode(SIZE)
# Creaiamo il gruppo di sprite che conterrà solo i blocchi.
# Questo blocco deve essere passato come argomento al metodo spritecollide
block_list = pygame.sprite.Group()
# Creiamo il gruppo che conterrà tutti gli sprite del gioco, incluso Hammer.
# Questo gruppo verrà usato per visualizzare tutti gli sprite visibili nell'area di gioco.
sprite_group = pygame.sprite.Group()
hammer = Hammer()
sprite_group.add(hammer)
for x in range (10):
# Creaiamo un valore casuale che corrisponde a un indice tra 0 e 2
indice=random.randint(0,2)
colore=colori[indice]
blocco = Blocco(colore, 30, 30)
# Impostiamo una posizione casuale per il blocco creato
blocco.rect.x = random.randrange(1170)
blocco.rect.y = random.randrange(339)
# Aggiungiamo ai gruppo gli sprite di tipo blocco creati
block_list.add(blocco)
sprite_group.add(blocco)
# Gestiamo gli eventi prodotti dal giocatore
while True:
for event in pygame.event.get():
# Interrompiamo il gioco se clicchiamo sulla X di fine gioco
if event.type == pygame.QUIT:
pygame.quit()
quit()
# Impostiamo la posizione di HAMMER attraverso il movimento del mouse
pos = pygame.mouse.get_pos()
# I controlli seguenti limitano i movimenti di HAMMER solo nella sezione di gioco
if pos[0]>0 and pos[0]<1156 and pos[1]>50 and pos[1]<320:
hammer.rect.x=pos[0]-5
hammer.rect.y=pos[1]-50
else:
if pos[1]<=50:
hammer.rect.y=0
elif pos[1]>=320:
hammer.rect.y=268
if pos[0]<=0:
hammer.rect.x=0
elif pos[0]>=1156:
hammer.rect.x=1150
# Se Hammer interseca un blocco, il suo riferimento viene aggiunto alla lista
# blocks_hit_list e poi viene eliminato dalla memoria, quindi verrà rimosso anche
# dai gruppi block_list e sprite_group.
blocks_hit_list = pygame.sprite.spritecollide(hammer, block_list, True)
# Disegniamo l'immagine come sfondo del gioco
screen.blit(SFONDO,(0,0))
# Disegniamo tutti gli sprite associati al gruppo sullo schermo
sprite_group.draw(screen)
# Aggiorniamo lo schermo per vedere i cambiamenti
pygame.display.update()
# Avvia il programma eseguendo il metodo main()
if __name__ == '__main__':
main()
Eseguendo il programma Python e puntando Hammer con il mouse, ogni volta che il martelletto intersecherà un blocco, lo sprite verrà eliminato dall'area di gioco:
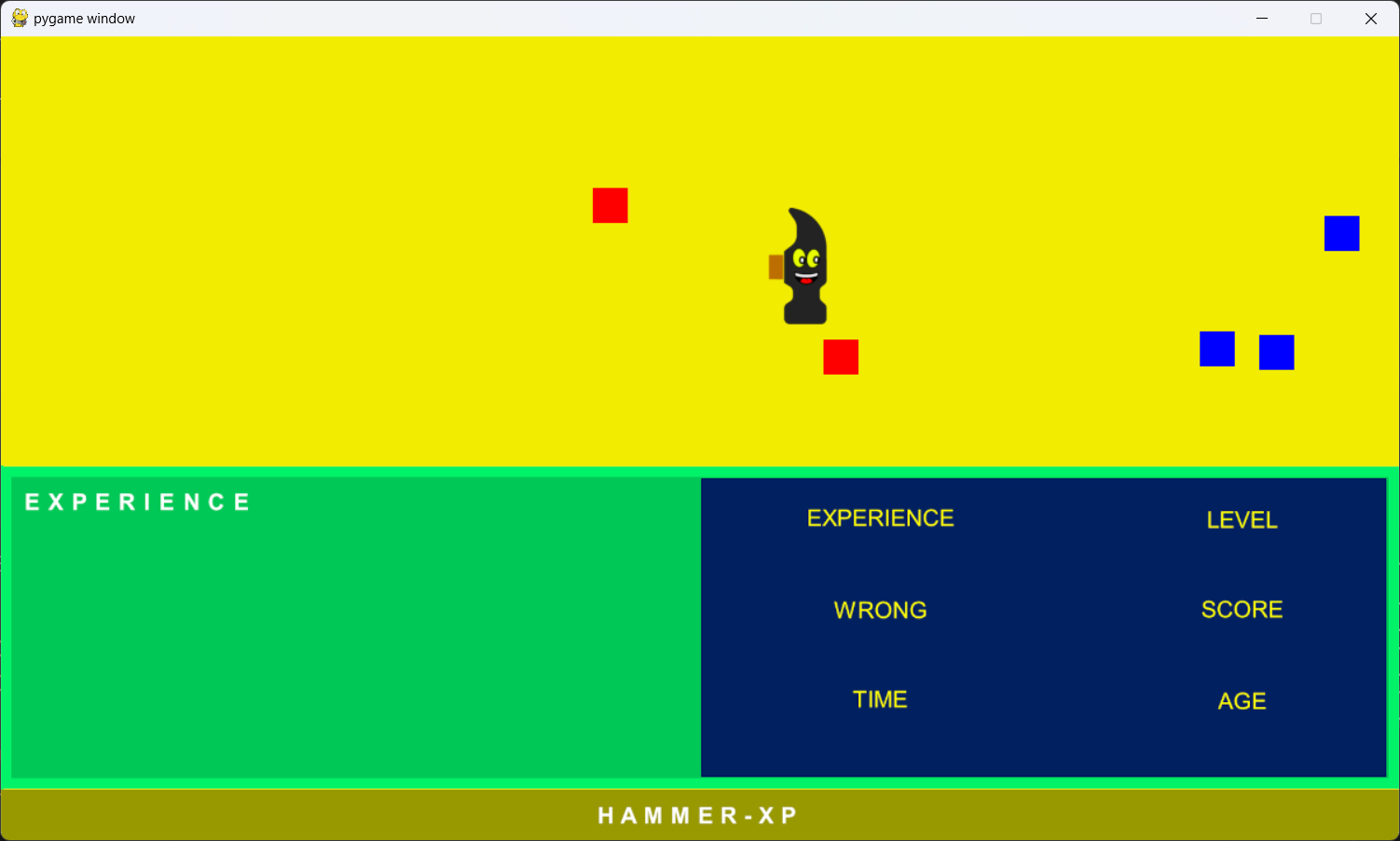
Nella prossima lezione vedrete come implementare un'esperienza reale con cui gli studenti potranno confrontarsi con l'obiettivo di dimostrare il loro livello di conoscenza sull'argomento proposto.
Per il download delle risorse di questa lezione cliccate qui.
< LEZIONE PRECEDENTE | LEZIONE SUCCESSIVA > | VAI ALLA PRIMA LEZIONE
T U T O R I A L S S U G G E R I T I
- Competenze per programmare
- Impariamo Python giocando al "Solitario del ferroviere"
- Impariamo a programmare con JavaScript
- Laboratori di Logica di programmazione in C
- Introduzione alla Logica degli oggetti
- Ricominciamo ... dal Linguaggio SQL
- APP Mania
- Come sviluppare un Sito con Wordpress
PER IMPARARE A PROGRAMMARE, SEGUI LE PLAYLIST SUL NOSTRO CANALE YOUTUBE "SKILL FACTORY CHANNEL": clicca qui per accedere alle playlist
PAR GOL (Garanzia di Occupabilità dei Lavoratori)

Se sei residente in Campania e cerchi lavoro, sai che puoi partecipare gratuitamente ad un corso di formazione professionale PAR GOL?
I corsi di formazione professionale PAR GOL sono finanziati dalla Regione Campania e ti permettono di acquisire una Qualifica Professionale Europea (EQF) e di partecipare ad un tirocinio formativo aziendale.
Invia il tuo CV o una manifestazione d'interesse a: recruiting@skillfactory.it
oppure
chiama ai seguenti numeri di telefono:
Tel.: 081/18181361
Cell.: 327 0870141
oppure
Contattaci attraverso il nostro sito: www.skillfactory.it
Per maggiori informazioni sul progetto PAR GOL, clicca qui.
Per maggiori informazioni sulle Qualifiche Professionali Europee (EQF), clicca qui.
Academy delle professioni digitali
Per consultare il catalogo dei corsi online della nostra Academy ...

... collegati al nostro sito: www.skillfactory.it
Come progettare e sviluppare giochi per l'educazione e la formazione con Python: lezione 2
![]() Mirko Onorato |
Mirko Onorato |
 Skill Factory - 18/06/2024 17:09:29 | in Tutorials
Skill Factory - 18/06/2024 17:09:29 | in Tutorials
Nella lezione precedente abbiamo visto gli step fondamentali per creare un gioco digitale da utilizzare nel mondo della scuola o della formazione professionale, per educare e facilitare l'apprendimento degli studenti.
In questa nuova lezione inizieremo a creare un semplice gioco digitale; l'obiettivo delle attività svolte in questa prima parte è quello di prendere confidenza con gli sprite.

Gli sprite sono oggetti che possono contenere immagini, vengono usati per creare le animazioni dei giochi.
Il protagonista del gioco sarà Hammer un martelletto che avrà lo scopo di eliminare dalle scene del gioco gli elementi non corretti.

Lo scopo del gioco sarà quello di verificare se gli studenti conoscono gli argomenti delle diverse esperienze di gioco proposte; ogni esperienza potrà prevedere anche più livelli.
Il gioco è adatto agli studenti della scuola elementare o media di età compresa tra gli otto e gli undici anni, naturalmente le esperienze di gioco possono essere create in base all'età. Quindi possiamo prevedere che il giocatore prima d'iniziare a giocare imposti la sua età.
L'immagine seguente mostra il mockup dell'interfaccia del gioco HAMMER-XP:

COME TRASFORMARE HAMMER IN UNO SPRITE
Prima di tutto vi suggerisco di creare una directory sul disco C, con il nome HAMMER-XP.
Per il download di HAMMER cliccate qui per visualizzare l'immagine, poi premete il tasto destro del mouse e salvate l'immagine di HAMMER nella directory HAMMER-XP.
Il codice Python seguente vi permetterà di trasformare HAMMER in uno sprite e visualizzarlo sullo schermo:
import pygame
SIZE = WIDTH, HEIGHT = 1200, 690 # Impostiamo la larghezza e l'altezza dello schermo
BACKGROUND_COLOR = pygame.Color('white') # Impostiamo il colore dello sfondo dello schermo
# La classe seguente permette di creare lo sprite e le sue caratteristiche
class Hammer(pygame.sprite.Sprite):
def __init__(self):
super(Hammer, self).__init__()
self.images = []
self.images.append(pygame.image.load('hammer.png')) # Associamo allo sprite l'immagine di hammer
self.index = 0
self.x=0
self.y=0
self.image = self.images[self.index]
self.rect = self.image.get_rect()
def main():
# Inizializziamo l'ambiente pygame
pygame.init()
# Impostiamo le dimensioni dello schermo
screen = pygame.display.set_mode(SIZE)
# Creiamo lo sprite hammer usando la classe sprite Hammer
hammer = Hammer()
# Creiamo il gruppo che contiene gli sprite del gioco
sprite_group = pygame.sprite.Group()
# Aggiungiamo al gruppo lo sprite hammer
sprite_group.add(hammer)
# Gestiamo gli eventi prodotti dal giocatore
while True:
for event in pygame.event.get():
# Interrompiamo il gioco se clicchiamo sulla X di fine gioco
if event.type == pygame.QUIT:
pygame.quit()
quit()
# Impostiamo la posizione di HAMMER nello schermo
hammer.rect.x=550
hammer.rect.y=150
# Impostiamo il colore dello sfondo dello schermo
screen.fill(BACKGROUND_COLOR)
# Disegniamo tutti gli sprite associati al gruppo sullo schermo
sprite_group.draw(screen)
# Aggiorniamo lo schermo per vedere i cambiamenti
pygame.display.update()
# Avviamo il programma eseguendo il metodo main()
if __name__ == '__main__':
main()
Avviando il programma otterrete la schermata seguente:
COME AGGIUNGERE AL GIOCO UN'IMMAGINE DI SFONDO
Per il download dell'immagine di sfondo del gioco cliccate qui per visualizzare l'immagine, poi premete il tasto destro del mouse e salvate l'immagine dello sfondo nella directory HAMMER-XP.
Il codice Python seguente vi permetterà di aggiungere al gioco anche l'immagine di sfondo:
import pygame
SIZE = WIDTH, HEIGHT = 1200, 690 # Impostiamo la larghezza e l'altezza dello schermo
# Carichiamo l'immagine di sfondo del gioco
SFONDO = pygame.image.load("sfondo_hammer_xp.png")
# La classe seguente permette di creare lo sprite e le sue caratteristiche
class Hammer(pygame.sprite.Sprite):
def __init__(self):
super(Hammer, self).__init__()
self.images = []
self.images.append(pygame.image.load('hammer.png')) # Associamo allo sprite l'immagine di hammer
self.index = 0
self.x=0
self.y=0
self.image = self.images[self.index]
self.rect = self.image.get_rect()
def main():
# Inizializziamo l'ambiente pygame
pygame.init()
# Impostiamo le dimensioni dello schermo
screen = pygame.display.set_mode(SIZE)
# Creiamo lo sprite hammer usando la classe sprite Hammer
hammer = Hammer()
# Creiamo il gruppo che contiene gli sprite del gioco
sprite_group = pygame.sprite.Group()
# Aggiungiamo al gruppo lo sprite hammer
sprite_group.add(hammer)
# Gestiamo gli eventi prodotti dal giocatore
while True:
for event in pygame.event.get():
# Interrompiamo il gioco se clicchiamo sulla X di fine gioco
if event.type == pygame.QUIT:
pygame.quit()
quit()
# Impostiamo la posizione di HAMMER nello schermo
hammer.rect.x=550
hammer.rect.y=150
# Disegniamo l'immagine come sfondo del gioco
screen.blit(SFONDO,(0,0))
# Disegniamo tutti gli sprite associati al gruppo sullo schermo
sprite_group.draw(screen)
# Aggiorniamo lo schermo per vedere i cambiamenti
pygame.display.update()
# Avvia il programma eseguendo il metodo main()
if __name__ == '__main__':
main()
Avviando il programma otterrete la schermata seguente:
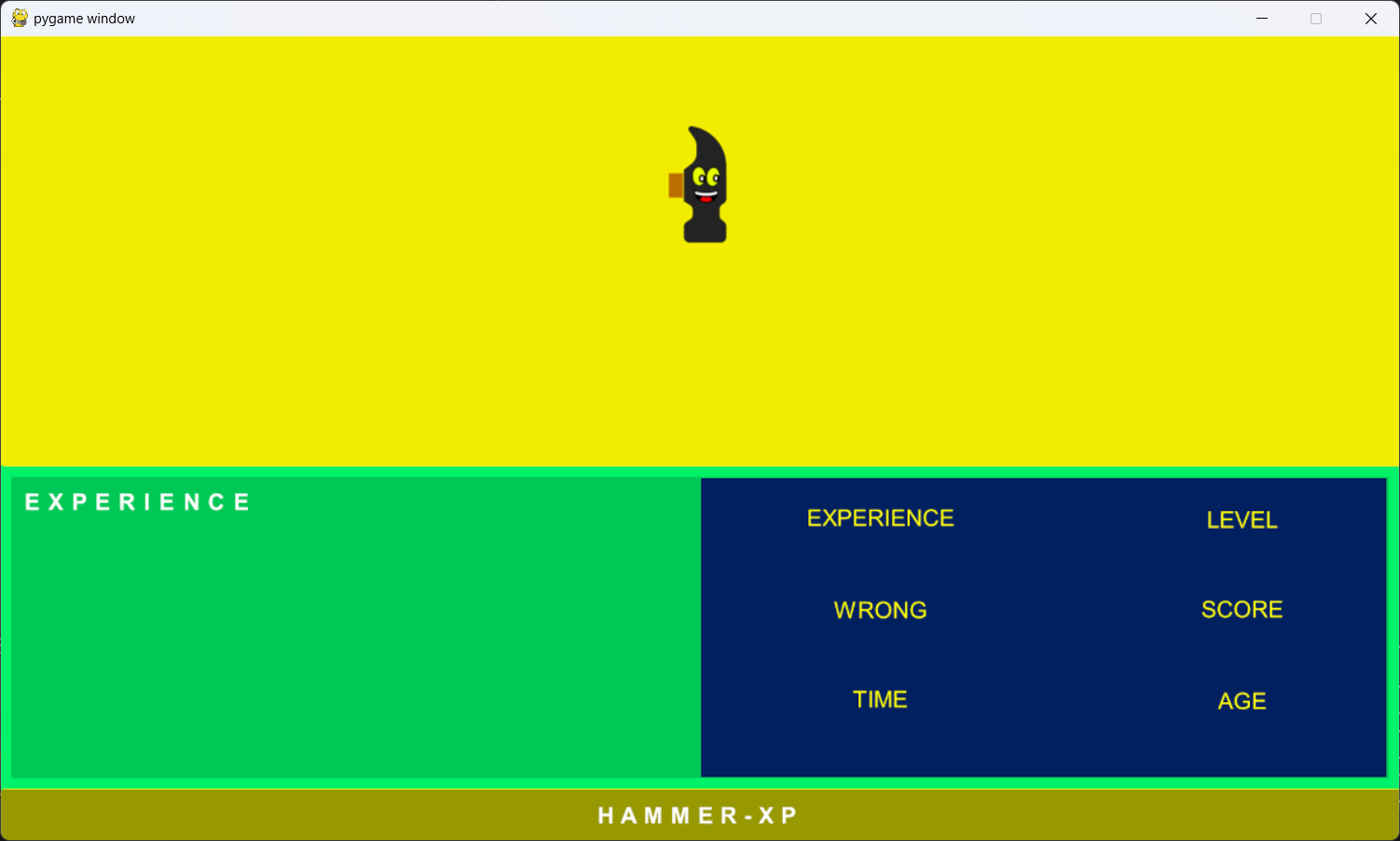
Per il download delle risorse di questa lezione cliccate qui.
< LEZIONE PRECEDENTE | LEZIONE SUCCESSIVA > | VAI ALLA PRIMA LEZIONE
T U T O R I A L S S U G G E R I T I
- Competenze per programmare
- Impariamo Python giocando al "Solitario del ferroviere"
- Impariamo a programmare con JavaScript
- Laboratori di Logica di programmazione in C
- Introduzione alla Logica degli oggetti
- Ricominciamo ... dal Linguaggio SQL
- APP Mania
- Come sviluppare un Sito con Wordpress
PER IMPARARE A PROGRAMMARE, SEGUI LE PLAYLIST SUL NOSTRO CANALE YOUTUBE "SKILL FACTORY CHANNEL": clicca qui per accedere alle playlist
PAR GOL (Garanzia di Occupabilità dei Lavoratori)

Se sei residente in Campania e cerchi lavoro, sai che puoi partecipare gratuitamente ad un corso di formazione professionale PAR GOL?
I corsi di formazione professionale PAR GOL sono finanziati dalla Regione Campania e ti permettono di acquisire una Qualifica Professionale Europea (EQF) e di partecipare ad un tirocinio formativo aziendale.
Invia il tuo CV o una manifestazione d'interesse a: recruiting@skillfactory.it
oppure
chiama ai seguenti numeri di telefono:
Tel.: 081/18181361
Cell.: 327 0870141
oppure
Contattaci attraverso il nostro sito: www.skillfactory.it
Per maggiori informazioni sul progetto PAR GOL, clicca qui.
Per maggiori informazioni sulle Qualifiche Professionali Europee (EQF), clicca qui.
Academy delle professioni digitali
Per consultare il catalogo dei corsi online della nostra Academy ...

... collegati al nostro sito: www.skillfactory.it





 Le Tue Aule
Le Tue Aule
 I Tuoi Gruppi
I Tuoi Gruppi
 Le Tue Selezioni
Le Tue Selezioni



 Scheda Azienda
Scheda Azienda








