I numeri che usiamo si chiamano "Numeri reali", in base alle loro caratteristiche li possiamo organizzare nei seguenti insiemi:

I numeri, sia interi (relativi), sia decimali (razionali), servono per esprimere rispettivamente quantità intere o frazionarie.

Sono irrazionali i numeri che non si possono indicare attraverso il rapporto tra numeri interi, come ad esempio il pi greco, che indica il rapporto tra la misura della circonferenza di un cerchio e il suo diametro oppure il numero di Nepero (e).

In programmazione per indicare la parte decimale di un numero si usa il punto "." al posto della virgola ",", quindi negli esempi userò questa convenzione.

Esempio 1

Per indicare la quantità di auto nell'immagine seguente, basta usare il numero intero 9:

mentre per indicare la quantità di auto nell'immagine seguente, bisogna usare il numero decimale 8.5, perché l'ultima auto è divisa a metà:

Esempio 2

Il risultato dell'espressione 10/2 è 5 che è un numero intero, perché il numero 10 può essere diviso esattamente in due parti intere, ciascuna composta da 5 unità.

Il risultato dell'espressione 10/3 è 3.33333 che è un numero decimale, perché il numero 10 può essere diviso in 3 parti intere, ciascuna composta da 3 unità, ma ne resta una che deve essere frazionata in 3 parti decimali da 0.33333.

Attenti, quando la quantità di cifre decimali di un numero è indefinita, ovvero quando l'unità non è divisibile in parti esattamente uguali, come nel caso del riusultato della divisione 10/3 = 3.33333..., il numero può essere scritto nel modo seguente:

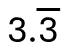
e si legge 3.3 periodico, perché il numero di 3 della parte decimale potrebbe essere infinito.

In programmazione, quando il numero di decimali è periodico, bisogna indicare la precisione del numero ovvero il numero di cifre da indicare dopo la virgola, per questo motivo nei linguaggi di programmazione si fa la distinzione tra numeri decimali a singola precisione (float) e doppia precisione (double). Di solito i numeri a doppia precisione si usano in ambiti scientifici, quelli a singola precisione per tutti gli altri ambiti.

Esempio 3 

I numeri si possono anche rappresentare sugli assi cartesiani, come mostra l'immagine seguente:

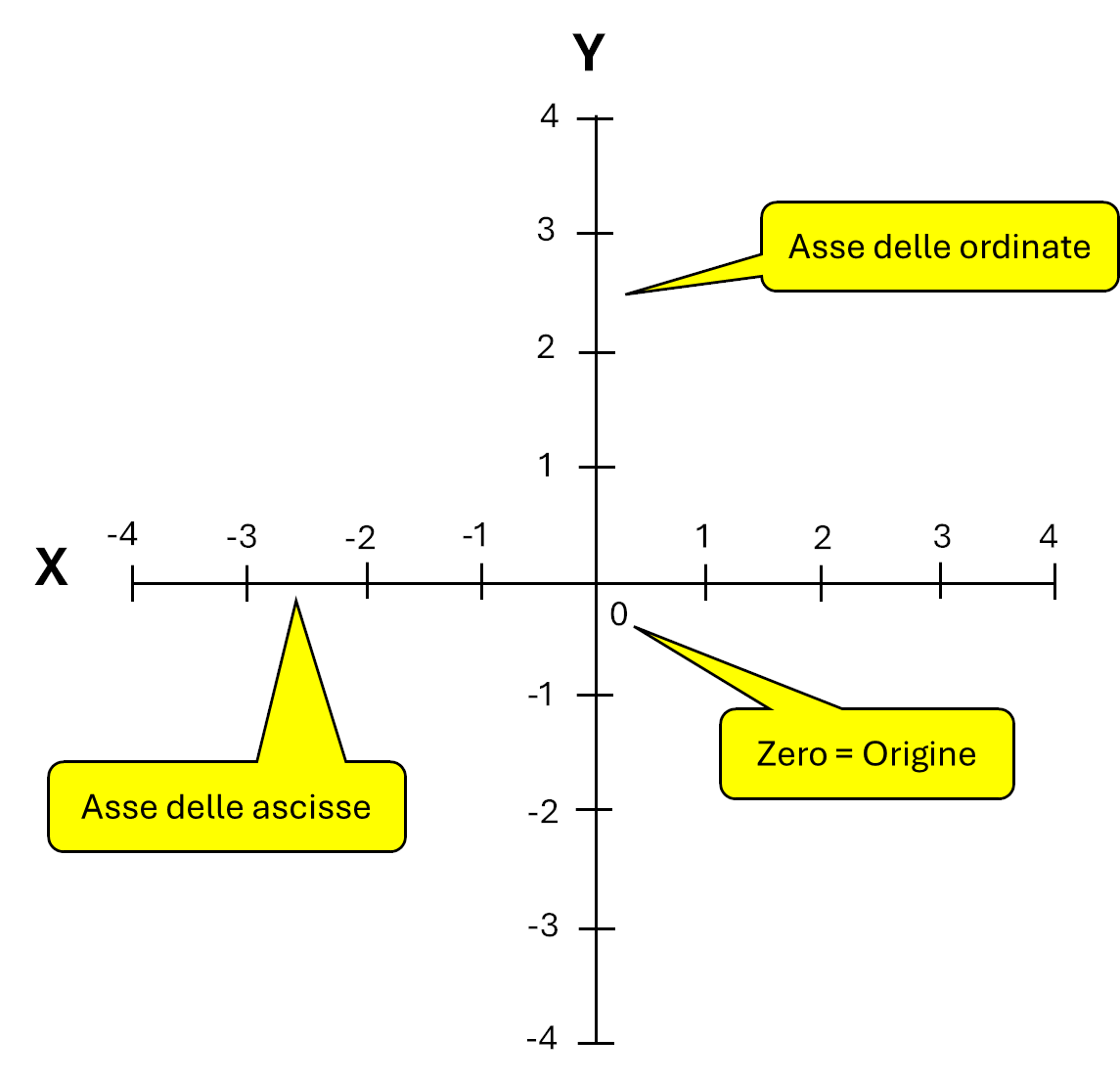
Se l'asse cartesiano è orizzontale si chiama asse delle ascisse e si indica con la lettera X, mentre se è verticale si chiama asse delle ordinate e si indica con la lettera Y.

Un piano su cui si disegna sia l'asse delle "Ascisse", sia l'asse delle "Ordinate" viene detto "Piano Cartesiano".

Il numero 0, si trova nel punto in cui gli assi X e Y s'incontrano e viene chiamato origine. Lo zero divide i numeri positivi (segno +) da quelli negativi (segno -) di entrambi gli assi; sia i numeri positivi, sia i numeri negativi sono infiniti.

Attenti, quando scrivete un numero positivo, non siete obbligati ad indicare il segno +, mentre quando scrivete un numero negativo il segno - è obbligatorio.

Sugli assi cartesiani, la parte decimale di un numero è sempre compresa nel segmento che unisce due numeri interi consecutivi. 

L'immagine seguente mostra la posizione del numero 2.5 sull'asse X:

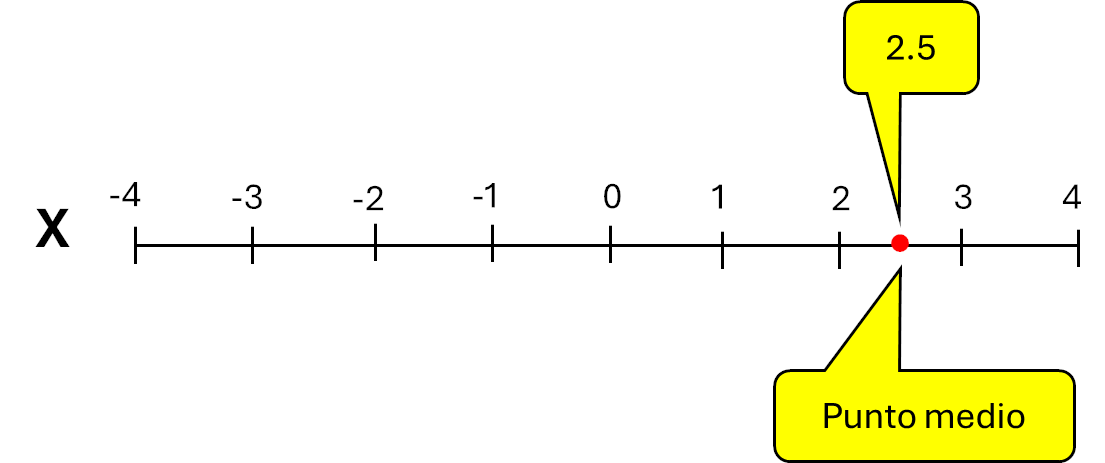
Ricordate che il punto centrale di un segmento che lo divide in due parti uguali è detto punto medio.

L'immagine seguente mostra la posizione del il numero -3.2 sull'asse X:

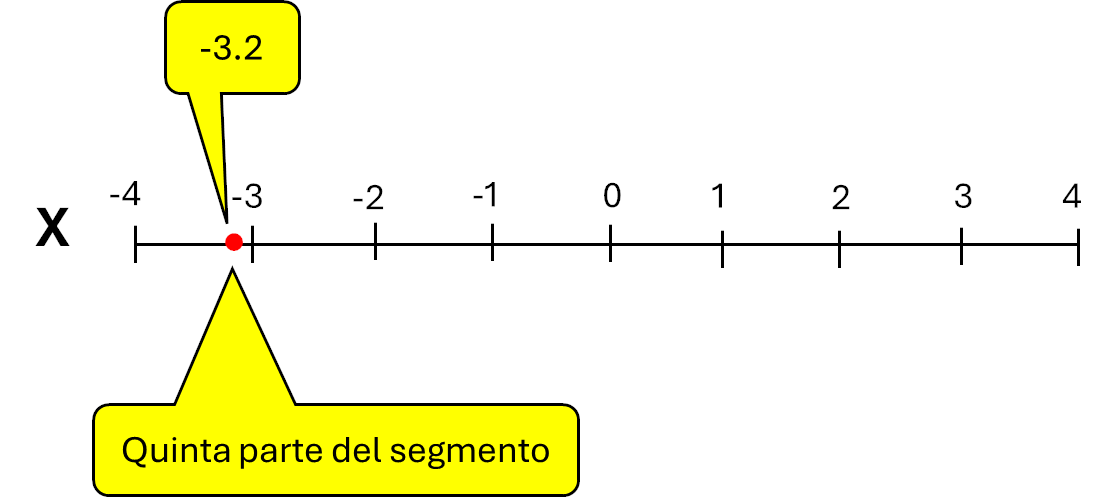
Per indicare la parte decimale 0.2 dovete posizionarvi esattamente nel punto che corrisponde alla quinta parte del segmento, perché 1/5=0.2, come mostra l'immagine.

Come ci ha insegnato il filosofo greco Democrito, un segmento può essere diviso infinite volte, per questo motivo la quantità di cifre decimali di un numero può anche essere molto grande; maggiore è il numero di decimali, tanto maggiore è il numero di volte che vengono divise le parti del segmento. La precisione, ovvero la quantità di cifre decimali di un numero, serve per capire fino a quando dobbiamo continuare  dividere le parti del segmento, per evitare di continuare all'infinito.  

In che modo i computer memorizzano i numeri interi?

I computer sono macchine elettroniche di tipo digitale, a differenza degli uomini, per scrivere i numeri possono usare solo due cifre: 0 e 1 chiamate bit (binary digit), per questo motivo usano il sistema di numerazione binario.  

I computer memorizzano i numeri nella RAM (Random Access Memory); la memoria ad accesso casuale composta da tanti interruttori, chiamati flip-flop, che permettono di scrivere i numeri in forma binaria - se l'interruttore spento (-) la cifra è zero, se è acceso (+) la cifra è uno. 

Clicca qui per conoscere la differenza tra mondo reale e mondo digitale.

Nei linguaggi di programmazione le variabili oppure gli oggetti che possono contenere tipi interi si dichiarano con: int oppure Integer, ad esempio:

int x=10;

Integer y=20;

In SQL le colonne di una tabella che possono contenere numeri interi di dichiarano con la parola chiave numeric, ad esempio:

create table magazzino(id numeric(7), quantita numeric(7),...);

Quando un computer memorizza nella RAM un numero intero, usa il primo bit a sinistra (quello più significativo) per indicare il segno; se il primo bit più significativo è 0 il numero intero è positivo, altrimenti è negativo. Gli altri bit servono per indicare il modulo del numero intero.

Per i numeri positivi, il modulo è rappresentato semplicemente dal valore binario del numero da memorizzare.

Per i numeri negativi, il modulo è rappresentato in complemento a 2.

2.147.483.647 = [0](segno)[1111111 11111111 11111111 11111111](modulo = valore binario del numero 2147483647)

–2.147.483.648  = [1](segno)[00000000 00000000 00000000 00000000](modulo = complemento a 2 del numero 2147483648)

Complemento a 2

Per calcolare il complemento a 2 di un numero binario è semplice, basta invertire i valori dei bit, gli zeri diventano uno e gli uno diventano zero e aggiungere 1 al numero che si ottiene.

Ad esempio, il complemento a 2 binario del numero 10 (decimale) si calcola nel modo seguente:

1) converto il numero 10 decimale in binario:

10 (decimale) = 1010 (binario)

2) Calcolo il complemento a 1 del numero 1010 invertendo gli zeri con uno e gli uno con zero:

1010 (binario) = 0101 (complemento a 1)

3) aggiungo 1 al numero 0101:

0101+
0001=
---------
 0110 (Complemento a 2 del numero binario 1010)

Allo stesso modo possiamo calcolare il complemento a 2 del numero decimale 2.147.483.648:

1) converto il numero 2.147.483.648 decimale in binario:

2.147.483.648 (decimale) = 10000000 00000000 00000000 00000000  (binario)

2) Calcolo il complemento a 1 del numero 10000000 00000000 00000000 00000000  invertendo gli zeri con uno e gli uno con zero:

10000000 00000000 00000000 00000000  (binario) = 01111111 11111111 11111111 11111111 (complemento a 1)

3) aggiungo 1 al numero 01111111 11111111 11111111 11111111:

01111111111111111111111111111111+
00000000000000000000000000000001=
-----------------------------------------------------------
10000000000000000000000000000000 (Complemento a 2 del numero binario 01111111111111111111111111111111)

 INFORMATICA APPLICATA

Laboratorio

Creare un programma che trasforma i numeri interi nella rappresentazione binaria a 32 bit usata dai computer per memorizzare le informazioni numeriche.

Soluzione JavaScript

// Funzioni
function convertiBinario(numeroIntero){
    let numeroBinario=[]
    let resto
    while (numeroIntero>1){
        resto=numeroIntero%2
        numeroBinario.push(resto)
        numeroIntero=Math.floor(numeroIntero/2)
    }
    numeroBinario.push(numeroIntero)
    for(let i=31-numeroBinario.length;i>0;i--){
        numeroBinario.push(0)
    }
    numeroBinario.reverse()
    return numeroBinario
}

function complemento2(numeroBinario){
    let inverti=[1,0]
    riporto=1
    for (let i=0;i<numeroBinario.length;i++){
        numeroBinario[i]=inverti[numeroBinario[i]]
    }
    for(let i=numeroBinario.length-1;i>0;i--){
        if (numeroBinario[i]==1 && riporto==1){
            numeroBinario[i]=0
            riporto=1
        }else if (numeroBinario[i]==1 && riporto==0){
            numeroBinario[i]=1
            riporto=0
        }else if (numeroBinario[i]==0 && riporto==1){
            numeroBinario[i]=1
            riporto=0
        }else{
            numeroBinario[i]=0
            riporto=0
        }
    }
}
// Programma
let input=require("readline-sync");
let numeroIntero=0
let numeroBinario=[]
let numeroBinarioStr=""
let segno=0
numeroIntero=parseInt(input.question("Numero intero: "))
while (numeroIntero<-2147483648 || numeroIntero> 2147483647){
    print("Errore: inserire un numero compreso tra -2147483648 e 2147483647")
    numeroIntero=parseInt(input.question("Numero intero: "))
}
if (numeroIntero<0){
    segno=1
    numeroBinario=convertiBinario(-(numeroIntero))
    complemento2(numeroBinario)
}
else if (numeroIntero>0){
    segno=0
    numeroBinario=convertiBinario(numeroIntero)
}
numeroBinarioStr="["+segno+"]["
for (let i=0;i<numeroBinario.length;i++){
    if (i<31){
        numeroBinarioStr+=numeroBinario[i]
    }
}
numeroBinarioStr+="]"
console.log(numeroBinarioStr)
 

Soluzione Python

# Funzioni

# Converte numero intero in binario
def convertiBinario(numeroIntero):
    numeroBinario=[]
    while numeroIntero>1:
        resto=numeroIntero%2
        numeroBinario.append(resto)
        numeroIntero=int(numeroIntero/2)
    numeroBinario.append(numeroIntero)
    for i in range(31-len(numeroBinario)):
        numeroBinario.append(0)
    numeroBinario.reverse()
    return numeroBinario

# Calcola il complemento a due di un numero binario
def complemento2(numeroBinario):
    inverti=[1,0]
    riporto=1
    for i in range(len(numeroBinario)):
        numeroBinario[i]=inverti[numeroBinario[i]]
    for i in range(len(numeroBinario)-1,0,-1):
        if numeroBinario[i]==1 and riporto==1:
            numeroBinario[i]=0
            riporto=1
        elif numeroBinario[i]==1 and riporto==0:
            numeroBinario[i]=1
            riporto=0
        elif numeroBinario[i]==0 and riporto==1:
            numeroBinario[i]=1
            riporto=0
        else:
            numeroBinario[i]=0
            riporto=0

# Programma
numeroIntero=0
numeroBinario=[]
segno=0
numeroIntero=int(input("Numero intero: "))
while numeroIntero<-2147483648 or numeroIntero> 2147483647:
    print("Errore: inserire un numero compreso tra -2147483648 e 2147483647")
    numeroIntero=int(input("Numero intero: "))
if numeroIntero<0:
    segno=1
    numeroBinario=convertiBinario(-(numeroIntero))
    complemento2(numeroBinario)
elif numeroIntero>0:
    segno=0
    numeroBinario=convertiBinario(numeroIntero)
print("["+str(segno)+"][",end="")
for i,x in enumerate(numeroBinario):
    if i<31: print(x,end="")
print("]")